
Knapsack 알고리즘 이란?
도둑이 보석가게에 배낭을 메고 침입했다.
배낭의 최대 용량은 W이며, 이를 초과해서 보석을 담으면 배낭이 터질 것이다.
각 보석들의 무게와 가격은 알고 있다.
배낭이 찢어지지 않는 선에서 가격 합이 최대가 되도록 보석을 담는 방법은?
위와 같은 문제를 해결하는대 사용되는 알고리즘을 대표적으로 Knapsack 알고리즘 이라고 부른다.
이러한 Knapsack 문제는 동적프로그래밍(DP)의 대표적인 문제로, 대부분의 알고리즘 서적에서 확인해볼수 있는 대표 유형이라 할 수 있다.
알고리즘의 분석
어떤 문제를 DP로 풀기 위해서는 '최적의 원리' (Principle of Optimality) 가 성립하는지를 확인해야 하는데, 최적의 원리란 다음과 같다.
"어떤 문제의 입력사례의 최적해가 그 입력사례를 분할한 부분사례에 대한 최적해를 항상 포함하고 있으면, 그 문제에 대하여 최적의 원리가 성립한다."
한마디로 전체의 최적해는 그 전체의 부분에서의 최적해를 포함하고 있다는 의미이다. Knapsack에서도 이 원리가 성립할까?
집합 S를 i개의 보석들 중에 최적으로 고른 부분집합이라고 가정하자.
우선 집합 S, 즉 OPT(i, w) 를 정의 해보자.
OPT(i, w) : 배낭 용량이 w일 때 아이템 1,2,...,i로 얻을 수 있는 최대 이득
case 1) 아이템 i를 선택하지 않는 경우 :
=> OPT(i, w) = OPT(i-1, w)
i번째 아이템을 선택하지 않을 경우의 최적해는 i번째 보석을 제외한 i-1 번까지의 보석으로 구성한 최적해와 동일한 값이된다.
따라서 i번째까지의 최적해 집합인 OTP(i, w)는 i를 포함하지 않는 i-1번 까지의 최적해 집합인 OTP(i-1, w)와 같은 것 이다.
case 2) 아이템 i를 선택한 경우 :
=> OPT(i) = vi + OPT(i-1, w-wi)
i번째 아이템을 선택하였다면, 기존의 i -1 까지의 최적해 집합인 OTP(i-1, w-wi)에 i번째 아이템의 value인 vi를 더해주면 된다.
주의할점은 i번째 아이템을 선택하고 가방에 넣을때 가방이 터지면안된다. 가방의 잔여 용량이 선택한 i번째 아이템보다는 크거나 같아야 한다.
지금까지의 이야기를 점화식으로 확인해 보자.
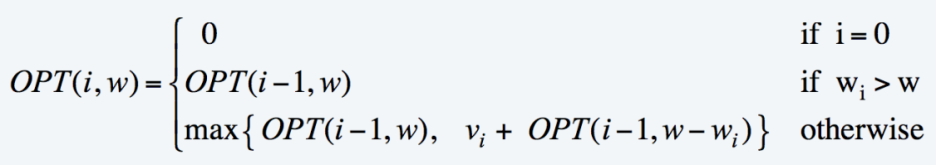
점화식의 의미는 다음과 같이 해석할 수 있다.
- i번째 보석이 배낭의 무게 한도보다 무거우면 넣을 수 없으므로 i번째 보석을 뺀 i-1개의 보석들을 가지고 구한 전 단계의 최적값을 그대로 가져온다
- 그렇지 않은 경우, i번째 보석을 위해 i번째 보석만큼의 무게를 비웠을 때의 최적값에 i번째 보석의 가격을 더한 값 or i-1개의 보석들을 가지고 구한 전 단계의 최적값 중 큰 것을 선택한다
이를 sudo code로 구현하면 다음과 같다. (n은 아이템의 수 이고, W는 가방의 용량이다. v는 보석의 value이다.)
다음 코드에서 M[i, w]는 OTP(i, w)와 동일한 의미를 갖는다.

예시
보석의 무게와 value가 다음과 같다고 해보자.
|
|
1
|
2
|
3
|
4
|
5
|
|
value
|
1
|
6
|
18
|
22
|
28
|
|
weight
|
1
|
2
|
5
|
6
|
7
|
가방은 weight을 11까지 버틸 수 있다. 이 문제를 어떻게 해결해야 할까?

1) 아이템을 0개 선택하였다면, 가방의 무게를 몇으로 잡던 최적해는 0뿐이다.
2) 1번 아이템을 선택한 경우, 가방의 무게가 증가해도 1짜리 하나밖에 담지 못함으로, 최적해는 전부 1이된다.
3) 1, 2번 아이템을 선택한 경우,
=> 가방의 크기가 1일때는 아이템 1번 만 담을수 있으니 최적해는 1이 된다.
문제는 가방의 용량이 2가 될 때 이다. 무게가 2이고 가치가 6인, 2번 아이템을 넣어야 더 효율적이다.
따라서 다음과 같은 코드가 실행된다.
OPT(2,2) = max( OTP(1,2), OTP(1, 0) + value[2] )이를 해석하면 배낭 용량이 2이고, 아이템 1, 2 를 사용할때의 최적해는
1번 보석만을 사용한 최적의 값 vs 2번째 보석을 위해 2번째 보석만큼의 무게를 비웠을 때(남은 가방의 용량은 0) 의 최적값에 2번째 보석의 value을 더한 값이 된다.
이러한 방식으로 전체 2중 loop를 돌면 최적해를 구할 수 있다.
관련된 문제로 백준의 12865번 평범한 배낭 문제를 추천한다.
'Algorithm > PS 알고리즘 정리' 카테고리의 다른 글
| [알고리즘] 트리의 지름 : Diameter of Tree (2) | 2022.01.20 |
|---|---|
| [알고리즘] Bipartite Graph : 이분 그래프 (0) | 2022.01.20 |
| [알고리즘] 조합 알고리즘 (0) | 2022.01.20 |
| [알고리즘] 다익스트라, 프림 알고리즘의 차이점 (0) | 2022.01.20 |
| [알고리즘] Union Find 알고리즘 : 경로 압축 (0) | 2022.01.20 |

댓글