
기존에도 Union Find 알고리즘을 사용하기는 했지만, 경로 압축을 하고있지 않아 시간이 조금더 걸리는 문제가 있었다.
간단하게 경로압축을 할 수 있는 방법을 배워 글을 써본다.
Union & Find
기본적인 Union Find 알고리즘의 구성은 다음과 같다.
int Find(int num){
if(parent[num] == num)
return num;
return Find(parent[num]);
}
void Union(int a, int b){
a = Find(a);
b = Find(b);
if(a != b)
parent[a] = b;
}맨 처음 parent 배열에서 각각은 자기 자신의 번호를 갖고 시작한다.
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
다음 숫자들이 Union 연산을 순서대로 진행한다고 해보자.
1 2 가 Union 연산을 진행한다.
Union(1, 2)
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
2
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
2 3
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
2
|
3
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
3 4
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
2
|
3
|
4
|
4
|
5
|
6
|
7
|
8
|
9
|
4 5
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
2
|
3
|
4
|
5
|
5
|
6
|
7
|
8
|
9
|
6 7
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
2
|
3
|
4
|
5
|
5
|
7
|
7
|
8
|
9
|
7 8
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
2
|
3
|
4
|
5
|
5
|
7
|
8
|
8
|
9
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
2
|
3
|
4
|
5
|
5
|
7
|
8
|
9
|
9
|

5번과 9번 자기 자신을 root로 하는 tree가 2개 생겼다.
1번 원소를 보면 2번 원소를 화살표로 가리키고있다. 이는 배열에서 1번 칸에 숫자 2가 담겨있는 의미를 나타낸 것 이다.
각 배열에 담긴 숫자는 자신의 부모를 나타내는 정보인 것 이다.
하지만 위와 같은 트리의 모양에는 문제점이 하나 있다. Tree의 높이가 너무 높다.
높이가 O(N)에 해당 되는 시간이 거려버린다.
이를 해결하기 위해 경로 압축을 하여 O(logN) 시간안에 해결하여 보자.
경로 압축 (Compression)
Find 의 알고리즘에서 조금만 수정을 해주면 경로압축이 가능하다.
int Find(int num){
if(parent[num] == num)
return num;
return parent[num] = Find(parent[num]);
}Find한 값을 배열에 저장후 반환해주는 것 이다.
예를 들어 설명하겠다. Union(3,4) 를 진행한 후, Unoin(1, 5)를 진행할 것 이다.
Union(3, 4) 까지 한 상황이라 해보자. 배열의 상황은 다음과 같다.
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
2
|
3
|
4
|
4
|
5
|
6
|
7
|
8
|
9
|
Find(5)의 경우 자기 자신이 root 이기 때문에 5가 금방 반환 된다.
하지만 Find(1) 의 경우 반환을 하면서 경로압축과정이 동반된다. 다음 그림을 확인해 보자.

Find 함수를 계속 호출하다보면 Find(4)를 호출하게 되고, 4는 자신이 root 이니 4를 반환할 것 이다.
4라는 값은 Find(3)을 호출할 때 다음과 같이 사용된다.
int Find(3){
if(parent[3] == 3)
return 3;
return parent[3] = Find(parent[3]);
}Find(parent[3]) 은 Find(4)와 같다. Find(4)는 4를 반환하니까, parent[3]에는 4라는 값이 저장되어 배열은 다음과 같아진다.
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
2
|
3
|
4
|
4
|
5
|
6
|
7
|
8
|
9
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
2
|
4
|
4
|
4
|
5
|
6
|
7
|
8
|
9
|
다음번에 Find(1)는 똑같이 진행하여 배열이 다음과 같아진다.
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
4
|
4
|
4
|
4
|
5
|
6
|
7
|
8
|
9
|
이제 Union(1, 5)에서 Find(1)과 Find(5)를 완성하였다.
이제 Union의 연산인 parent[4] = Find(5); 를 진행해주면 배열은 다음과 같아진다.
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
4
|
4
|
4
|
5
|
5
|
6
|
7
|
8
|
9
|
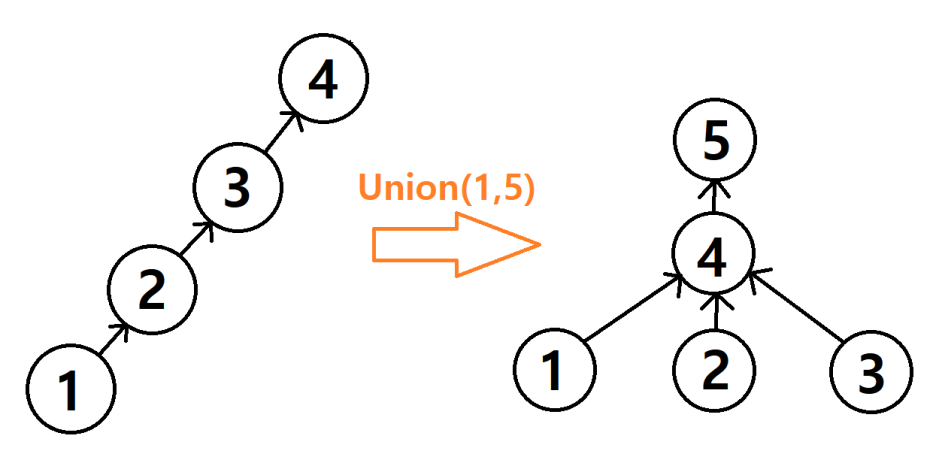
Tree의 모양또한 다음과 같이 바뀐것을 알 수 있다.
'Algorithm > PS 알고리즘 정리' 카테고리의 다른 글
| [알고리즘] 조합 알고리즘 (0) | 2022.01.20 |
|---|---|
| [알고리즘] 다익스트라, 프림 알고리즘의 차이점 (0) | 2022.01.20 |
| [알고리즘] Red-Black Tree : 레드 블랙 트리 (1) | 2022.01.19 |
| 코딩테스트 효과적인 C++ 코드 작성 팁 (0) | 2022.01.19 |
| STL을 사용한 그래프의 구현 : Graph implementation using STL (0) | 2022.01.15 |

댓글