
이분 그레프 (Bipartite Graph) 란?
우선 학교에서 공부할때 필기한 내용을 먼저 보인후, 이를 내가 설명하여 보겠다.

이분 그레프란 정점의 집합을 2개의 독립적인 집합으로 나눌 수 있으며, 나눠진 집합에서는 서로다른 집합 사이에만 간선이 존재하는 그레프를 의미한다.
즉 같은 집합 내부의 정점간에는 간선이 있으면 안된다.
이를 그림으로 표현하면 다음과 같음 그레프를 의미한다.

집합이 오른쪽(V)과 왼쪽(U) 2개의 집합으로 나뉘어 졌다.
간선들의 양끝 정점(u와 v) 또한 서로다른 집합에 포함되어있다. 정점 u는 집합 U에, 정점 v는 집합 V에 포함되어야 하는 것!
추가적으로 그림에는 없지만, 한쪽 집합에 그냥 정점 하나만 달랑 있어도 이분 그레프 라고 할 수 있다.
예시를 확인해 보자!!
Examples
1) 6개의 정점을 갖는 그레프
다음 그림과 같은 그레프가 있다고 해보자. 이 그레프는 Bipartite 할까?
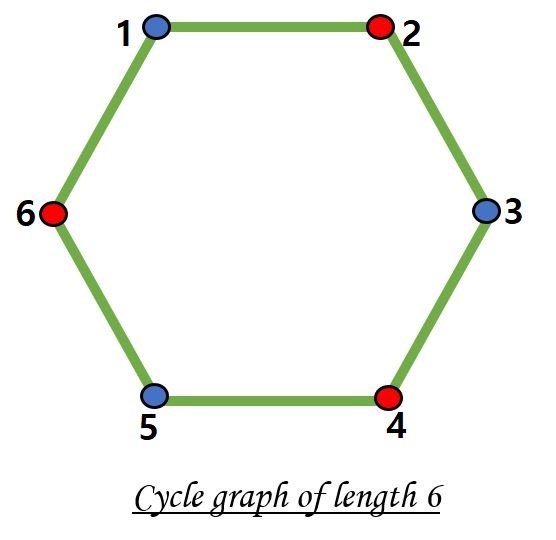
결론부터 말하면 Bipartite하다. 2개의 독립적인 집합으로 나눌 수 있으며, 간선은 서로다른 집합간에만 존재하게 된다!
위의 그레프를 집합으로 보면 다음고 같아진다.
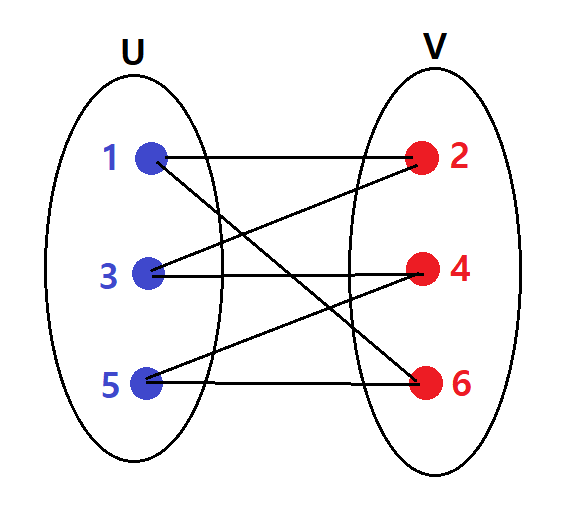
관련된 문제로는 백준의 1707번 문제를 추천한다.
1707번: 이분 그래프
입력은 여러 개의 테스트 케이스로 구성되어 있는데, 첫째 줄에 테스트 케이스의 개수 K가 주어진다. 각 테스트 케이스의 첫째 줄에는 그래프의 정점의 개수 V와 간선의 개수 E가 빈 칸을 사이에
www.acmicpc.net
'Algorithm > PS 알고리즘 정리' 카테고리의 다른 글
| [알고리즘] 에라토스테네스의 체 : 소수 판별법 (0) | 2022.01.21 |
|---|---|
| [알고리즘] 트리의 지름 : Diameter of Tree (2) | 2022.01.20 |
| [알고리즘] Knapsack Problem (0) | 2022.01.20 |
| [알고리즘] 조합 알고리즘 (0) | 2022.01.20 |
| [알고리즘] 다익스트라, 프림 알고리즘의 차이점 (0) | 2022.01.20 |

댓글