
조합 알고리즘 같은 경우 자주 사용한다는 글로 정리해두는 것 도 좋을것 같아 글을 작성해본다.
조합이란?
간단하게 0, 1, 2, 3, 4, 5 가 있다고 해보자.
이중 숫자 4개를 순서에 상관없이 선택하는 경우는 몇가지가 있는지를 파악하는 것 이다.
순서가 상관없으니, (0, 1, 2, 3) 과 (0, 1, 3, 2)는 같은 경우이다.
이는 DFS를 활용하여 구하면 된다.
생각의 흐름
tree를 그려보면서 생각해 보자.
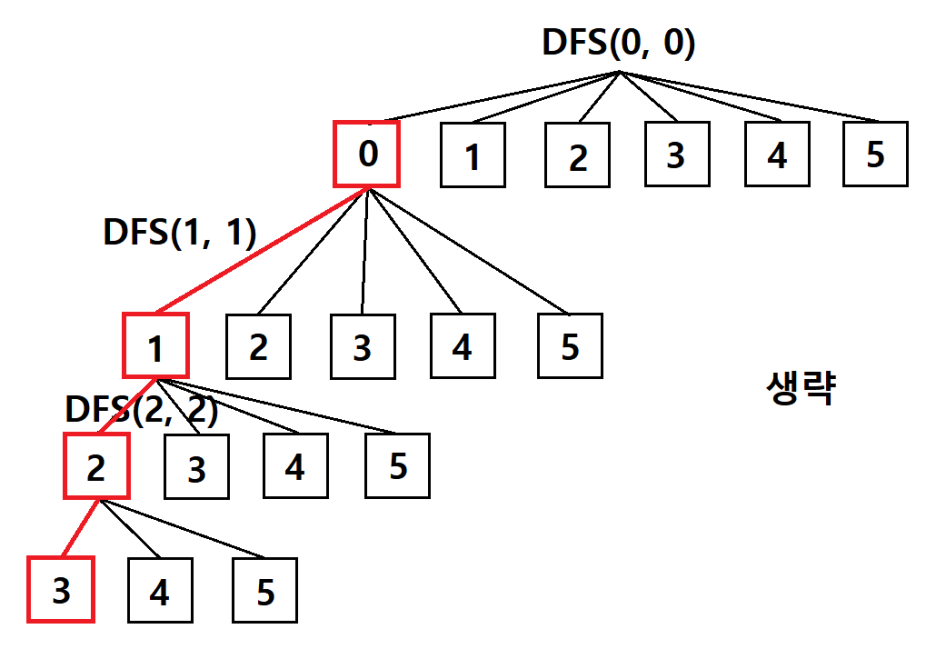
빨간 선만 따라서 DFS를 진행하면 (0, 1, 2, 3) 이라는 하나의 조합이 나온다.
그다음은 0, 1, 2, 4 또 그다음은 0, 1, 2, 5 까지 진행할 것 이며, 그다음에는 DFS(3, 2)가 호출되어 0, 1, 3, 4가 불러진다.
코드 구현
#include <bits/stdc++.h>
using namespace std;
int n, r;
int ch[20];
void DFS(int st, int lv){
if(lv == r){
for(int j=0; j<lv; j++)
cout << ch[j] << " ";
cout << "\n";
}else{
for(int i = st; i < n; i++){
ch[lv] = i;
DFS(st+1, lv+1);
}
}
}
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
freopen("input.txt", "rt", stdin);
cin >> n >> r;
DFS(0, 0);
return 0;
}'Algorithm > PS 알고리즘 정리' 카테고리의 다른 글
| [알고리즘] Bipartite Graph : 이분 그래프 (0) | 2022.01.20 |
|---|---|
| [알고리즘] Knapsack Problem (0) | 2022.01.20 |
| [알고리즘] 다익스트라, 프림 알고리즘의 차이점 (0) | 2022.01.20 |
| [알고리즘] Union Find 알고리즘 : 경로 압축 (0) | 2022.01.20 |
| [알고리즘] Red-Black Tree : 레드 블랙 트리 (1) | 2022.01.19 |

댓글