해당 본문의 원문의 출처는 Geeks for Geeks 입니다. STL을 활용한 Graph 구현방식의 공부에 도움이 될거라 생각합니다.

원문 주소
Graph implementation using STL for competitive programming | Set 1 (DFS of Unweighted and Undirected) - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
Graph implementation using STL for competitive programming | Set 2 (Weighted graph) - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
Graph implementation using STL for competitive programming | Set 1 (DFS of Unweighted and Undirected)
이번 글에서는 vector를 사용하여 유용하고 빠르게 그레프를 구현하는 방법에 대하여 알아봅시다.
구현은 인접 리스트를 활용하여 그레프를 표현하게 됩니다.
우선 다음 예시는 무방향이며 가중치가 없는 정점 5개의 그레프 입니다. 사진을 통해서 확인해 봅시다.
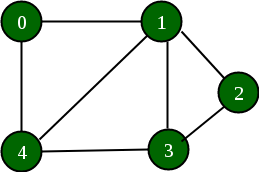
위의 그레프를 인접리스트로 표현하면 다음과 같습니다.
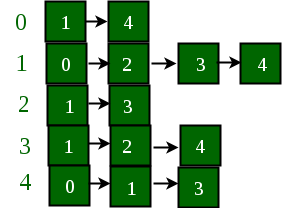
우리는 한가지 STL, 즉 vector를 사용해서 인접리스트 형식의 그레프를 구현할 것 입니다.
● vector : vector는 sequence container 입니다. 우리는 vector에 인접리스트의 정점들을 저장할 것 입니다. 또한 정점의 번호를 마치 vector의 index인것처럼 사용하게 됩니다.
이 idea는 그래프를 vector의 배열로 나타내는 것 입니다. 또한 모든 vector들은 인접리스트의 정점을 나타냅니다.
다음 코드는 STL을 활용하여 C++로 구현한 DFS순회의 코드 입니다. 이를 통해 확인해 봅시다.
// A simple representation of graph using STL,
// for the purpose of competitive programming
#include<bits/stdc++.h>
using namespace std;
// 간선을 추가해주는 함수
void addEdge(vector<int> adj[], int u, int v)
{ // 무방향 이니 양방향 모두 연결해줘야 한다.
adj[u].push_back(v);
adj[v].push_back(u);
}
// 주어진 u로부터 DFS탐색을 재귀적으로 진행하는 함수
void DFSUtil(int u, vector<int> adj[], vector<bool> &visited)
{
visited[u] = true;
cout << u << " ";
for (int i=0; i<adj[u].size(); i++)
if (visited[adj[u][i]] == false)
DFSUtil(adj[u][i], adj, visited);
}
// This function does DFSUtil() for all
// unvisited vertices.
void DFS(vector<int> adj[], int V)
{
vector<bool> visited(V, false);
for (int u=0; u<V; u++)
if (visited[u] == false)
DFSUtil(u, adj, visited);
}
// Driver code
int main()
{
int V = 5;
// The below line may not work on all
// compilers. If it does not work on
// your compiler, please replace it with
// following
// vector<int> *adj = new vector<int>[V];
vector<int> adj[V];
// Vertex numbers should be from 0 to 4.
addEdge(adj, 0, 1);
addEdge(adj, 0, 4);
addEdge(adj, 1, 2);
addEdge(adj, 1, 3);
addEdge(adj, 1, 4);
addEdge(adj, 2, 3);
addEdge(adj, 3, 4);
DFS(adj, V);
return 0;
}
Graph implementation using STL for competitive programming | Set 2 (Weighted graph)
위의 set1 에서는 가중치가 없는 그레프에 대하여 토론하였다. 이번 글에서는 STL을 활용한 가중치 그레프에 대하여 의논할 것 이다. 아! 물론 가중치 그레프의 구현은 이전과 마찬가지로 인접리스트로 구현할 것 이다.
가중치 그레프의 예시는 다음과 같다.

우리는 두가지 STL을 사용해서 그레프를 표현할 것 이다:
● vector : vector는 sequence container 입니다. 우리는 vector에 인접리스트의 정점들을 저장할 것 입니다. 또한 정점의 번호를 마치 vector의 index인것처럼 사용하게 됩니다.
● pair : 원소를 쌍으로 저장하기 위한 간단한 container입니다. 우리는 이를 활용하여 인접 정점의 번호와 간선의 가중치를 한 쌍으로 묶어 저장할 것 입니다.
아이디어는 vector pair의 vector를 활용하는 것 입니다. 다음 코드를 통해서 확인해 봅시다.
// C++ program to represent undirected and weighted graph
// using STL. The program basically prints adjacency list
// representation of graph
#include <bits/stdc++.h>
using namespace std;
// To add an edge
void addEdge(vector <pair<int, int> > adj[], int u, int v, int wt)
{
adj[u].push_back(make_pair(v, wt));
adj[v].push_back(make_pair(u, wt));
}
// Print adjacency list representaion ot graph
void printGraph(vector<pair<int,int> > adj[], int V)
{
int v, w;
for (int u = 0; u < V; u++)
{
cout << "Node " << u << " makes an edge with \n";
for (auto it = adj[u].begin(); it!=adj[u].end(); it++)
{
v = it->first;
w = it->second;
cout << "\tNode " << v << " with edge weight ="
<< w << "\n";
}
cout << "\n";
}
}
// Driver code
int main()
{
int V = 5;
vector<pair<int, int> > adj[V];
addEdge(adj, 0, 1, 10);
addEdge(adj, 0, 4, 20);
addEdge(adj, 1, 2, 30);
addEdge(adj, 1, 3, 40);
addEdge(adj, 1, 4, 50);
addEdge(adj, 2, 3, 60);
addEdge(adj, 3, 4, 70);
printGraph(adj, V);
return 0;
}결과값은 다음과 같습니다.
Node 0 makes an edge with
Node 1 with edge weight =10
Node 4 with edge weight =20
Node 1 makes an edge with
Node 0 with edge weight =10
Node 2 with edge weight =30
Node 3 with edge weight =40
Node 4 with edge weight =50
Node 2 makes an edge with
Node 1 with edge weight =30
Node 3 with edge weight =60
Node 3 makes an edge with
Node 1 with edge weight =40
Node 2 with edge weight =60
Node 4 with edge weight =70
Node 4 makes an edge with
Node 0 with edge weight =20
Node 1 with edge weight =50
Node 3 with edge weight =70
해당 본문은 저 스스로 공부하면서 간단하게 번역한 글입니다. 이공계라 영어사용이 자유롭게 되지는 않습니다만... 누군가 이글이 도움이 될수 있길 희망하며... 간단하게 옮겨봅니다.
'Algorithm > PS 알고리즘 정리' 카테고리의 다른 글
| [알고리즘] 조합 알고리즘 (0) | 2022.01.20 |
|---|---|
| [알고리즘] 다익스트라, 프림 알고리즘의 차이점 (0) | 2022.01.20 |
| [알고리즘] Union Find 알고리즘 : 경로 압축 (0) | 2022.01.20 |
| [알고리즘] Red-Black Tree : 레드 블랙 트리 (1) | 2022.01.19 |
| 코딩테스트 효과적인 C++ 코드 작성 팁 (0) | 2022.01.19 |

댓글