해당 본문은 학교수업시간에 배운 강의내용을 기반으로 정리하는 요약글 입니다. 정확하지 않은 점이 있으면 지적해주시면 감사하겠습니다.

이번시간에는 우선순위 큐 (priority queue)에 대하여 배웠다.
일반적인 queue는 후입 선출의 과정, 즉 먼저 들어간 원소가 먼저 나오는 방식이지만
우선순위 큐는 각 원소마다 우선순위가 정해져서, 우선순위가 높은 원소부터 먼저 나오는 방시이다.
Priority Queue
- Queue 이긴 한데, 원소들이 우선순위를 갖고있다.
- 우선순위가 높은 원소가 먼저 나온다.
- 가능한 배열 구현 종류
- Sorted by priority : 빠른 삭제연산, 하지만 삽입이 느리다.
- Unsorted : 빠른 삽입연산, 하지만 삭제가 느리다.
Priority Queue 의 구현
우선순위 큐는 어떤 자료구조를 활용하여 구현해야 할까?
이전시간에 배운 AVL, 2-3-4 or Red-Black Tree를 활용해야 할까?
물론 이들을 활용하여 구현한다면 Search가 O(logN) 안에 가능하니 만족할만한 결과가 나올수 있다.
하지만 더 좋은 방법이 있다. 바로 Heap 이라는 자료구조를 사용하는 것 이다.
Heap
● Heap은 완전이진트리(Complete Binary Tree) 이어야 한다.
- 마지막 level을 제외한 모든 level에서는 원소들이 가득 차 있어야 한다.
- 마지막 level에서는 왼쪽부터 채워야 한다.
그림을 통해 보면 좀더 명확하게 이해된다.

● Heap property 를 만족해야한다.
다음 그림의 경우 key값이 클수록 우선순위가 높은 max-heap 에 해당된다.

● Heap의 구현
Heap은 1차원 배열을 이용하여 구현이 가능하다.
- 루트 노드 A[1].
- A[i]의 부모 = A[i/2]
- A[i]의 왼쪽 자식 = A[2i]
- A[i]의 오른쪽 자식 = A[2i+1]

● Heap의 Insert / Delete
1) Insert
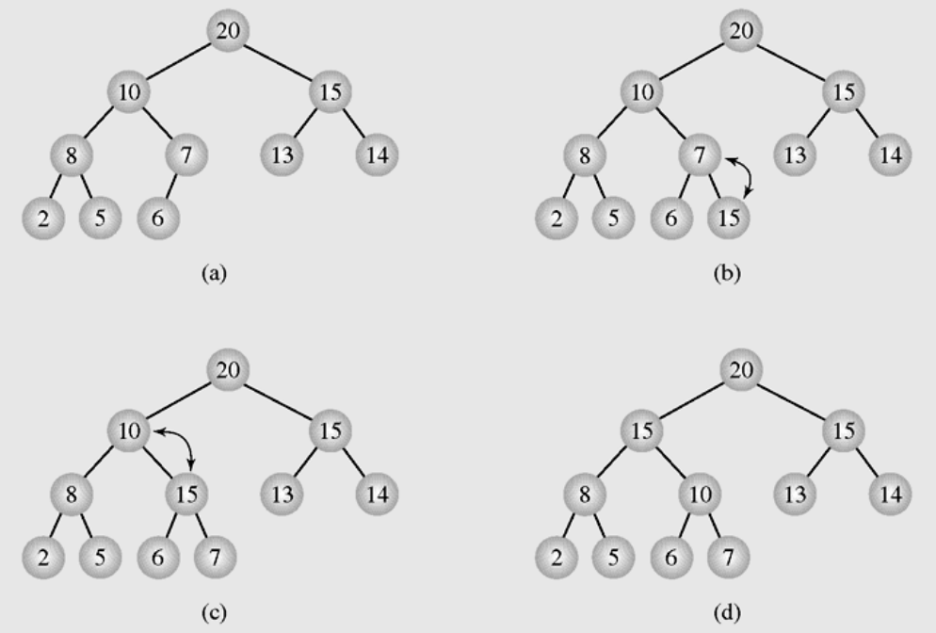
위의 그림을 예로 설명해보자.
(a) 의 상황에서 key값으로 15를 갖는 노드를 추가한다고 하자. 우선 트리의 맨 끝부분(배열에서 마지막 자리) 에 15를 삽입시킨다.
이후 삽입한 자리의 부모노드(key값 7)과 비교한다.
15의 값이 더 크기때문에 부모와 자식의 위치를 교환한다. (c)의 상황이 된다.
다시 15는 새로운 부모인 10과 비교한다. 15가 더 크기에 교환하면 (d)와 같은 상황이 된다.
15는 새로운 부모인 20보다 작기때문에 자신의 자리를 찾게되었다.
2) Delete

(a)의 상황에서 삭제를 한다면 heap은 우선순위가 가장 높은 20부터 추출한다.
20이 제거된다면 20의 자리가 empty 상황이 된다. 이를 어떻게 해결할 것 인가? 자식을 끌어다 올려야 하나?
간단한 방법은 맨 마지막 원소인 6을 root의 빈 자리에 전달하는것 이다.
root에 전달된 6은 자신의 자식과 비교하면서 교환하면서 내려가 자신의 자리를 찾게된다.
이는 Insert에서 위로 찾아가는 과정과 유사하다.
● 결론
Priority Queue는 O(logN)시간 안에 삽입과 삭제가 가능하다.
Dijkstra Algorithm
다익스트라 알고리즘은 그레프의 한 정점에서 나머지 모든 정점까지의 최단경로의 길이를 알고싶을때 사용하는 알고리즘이다
이에관한 글을 예전에 정리해둔적이 있으니 이를 참고하길!
[자료구조] C++로 쉽게 풀어쓴 자료구조 : 12장, 가중치 그래프
내돈내고 내가 공부한것을 올리며, 중요한 단원은 저 자신도 곱씹어 볼겸 가겹게 포스팅 하겠습니다. 이번 12장 책 코드에 중간중간 오류코드들이 보인다... 이해를 조금 방해하는 수준이다. 1) 12
blogshine.tistory.com
Dijkstra Proof
다익스트라 라는 알고리즘은 왜 작동할까? 이에관한 증명을 해보자.
일단 최단경로 에 대한 정의부터 몇가지 해보자.
1) 가중치 (방향) 그래프 G=(V,E), 즉 모든 edge에 가중치가 있음
2) 경로 p=(v0,v1,...,vk)의 길이는 경로상의 모든 edge의 가중치의 합
3) 노드 u에서 v까지의 최단경로의 길이를 δ(u, v)라고 표시하자.
최단경로를 구하기 위해 다익스트라 알고리즘의 입력값으로 음수 사이클이 없는 가중치 방향그레프 G=(V, E)와 출발노드 s를 넘겨준다.
s로부터의 최단경로의 길이를 이미 알아낸 노드들의 집합 S를 유지. 맨 처음엔 S = Ø
● Loop invariant:
u∉S인 각 노드 u에 대해서 d(u)는 이미 S에 속한 노드들만 거쳐서 s로부터 u까 지 가는 최단경로의 길이

d(u)는 출발점 s에서 이미 S에 속한 node들만 지난후, 마지막 한 edge를 추가하여 도착한 node u까지의 길이이다.
다음과 같은 주장이 있다고 해보자.
주장 :
d(u)=min v∉S d(v)인 노드 u에 대해서, d(u)는 s에서 u까 지의 최단경로의 길이이다.
즉 S에 속하지 않은 노드의 d값이 최소인 노드를 u라고 한다면, d(u)는 그냥 출발점에서 u까지 가는 최단경로의 길이이다.
증명: Proof by Contradiction
d(u)가 최단경로가 아니라고 가정해보자. 더 짧은것이 있다는 말이다.
그렇다면 그 경로는 집합 S에 속하지 않는 노드를 최소한 하나는 지나야 한다. 그 노드를 v라고 하자.
문제는 d(v) ≥ d(u) 라는 점 이다. 애초에 u를 d값이 최소인 node라고 했기 때문이다. 따라서 모순이 발생했다.

역이 모순이니, 맨처음한 가정이 참임을 알 수 있다.
이후 노드 u가 집합 S에 추가되고, u와 연결되있는 노드에 관하여 relaxation을 진행하면 loop invariant가 유지된다.
'CS > Data Structure (2021-1)' 카테고리의 다른 글
| [자료구조] The Halting Problem (정지 문제) (0) | 2023.03.05 |
|---|---|
| [자료구조] 2-3-4 Tree, Red-Black Tree (2) | 2022.01.25 |
| [자료구조] AVL Tree, 2-3 Tree (0) | 2022.01.25 |
| [자료구조] Binary Search Tree (0) | 2022.01.25 |
| [자료구조] Linked List (0) | 2022.01.25 |

댓글