해당 본문은 학교수업시간에 배운 강의내용을 기반으로 정리하는 요약글 입니다. 정확하지 않은 점이 있으면 지적해주시면 감사하겠습니다.
이번 시간에는 이진탐색트리 에 대하여 배우는 시간이였다.
이진탐색의 방식으로 만들어진 트리라고 생각하면 쉽다.
크게 Search, Insert, Delete 3가지 기능이 필요한데 Delete의 경우 삭제할 Node의 자식이 몇명인지에 따라 case가 나뉜다.
우선 Skip List에 대하여 간단하게 살펴보자.
Skip List
Skip LIst란 여러 node를 건너뛸 수 있는 Linked List를 말한다. 이를 활용하여 중간 지점으로 건너 뛸 수 있다면, 이진탐색의 방식을 Linked List에서도 사용이 가능해질 것 이다.
하지만 insert, delete와 같은 핵심 기능을 제공함과 동시에 이러한 연결리스트의 구조를 유지하기란 쉽지 않다.
데이터가 바뀌지 않을 때만 한정적으로 사용하기에도 적절치 않다. 배열이 더 효율적이다.
더 좋은 자료구조가 없을까?
Binary Search Tree
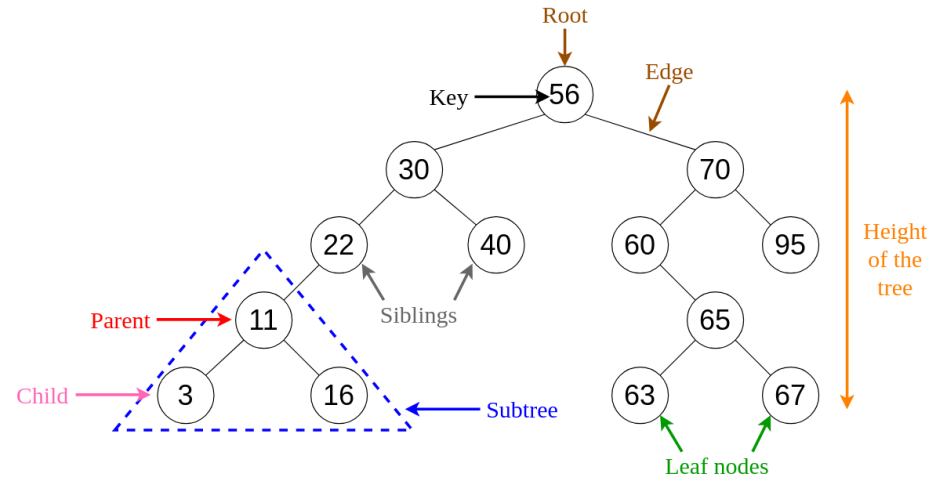
이진 탐색 트리의 정의부터 확인해 보면 다음과 같다.
- 노드들은 key값을 갖고있다.
- 하나의 Root Node가 있다.
- Root Node는 최대 2개의 자식 Node를 갖을 수 있다.
- 각각의 자식 Node들은 그 자신의 subtree의 root이다.
- 각각의 subtree들 또한 스스로 이진탐색트리(BST)이다.
- 한 BST에서 root의 왼쪽 subtree에 있는 Node의 key값들은 root의 key값보다 작으며, root의 오른쪽 subtree에 있는 Node들의 key값은 모두 root의 key보다 크다.
이진 탐색의 class를 구현하면 다음과 같을 것 이다.
첫 BST를 생성시, dummy Node를 만드는것을 볼 수 있다.
class BST {
Node* root;
public:
BST();
bool Search(int x, Node** P, Node** D);
bool Insert(int x);
bool Delete(int x);
void Print(Node* C, int depth, int LR);
};
BST::BST() {
root = new Node;
root->data = 999;
root->L = nullptr;
root->R = nullptr;
}
Node
각각의 Node마다 key값과 왼쪽 child Node를 가리킬 포인터 변수, 오른쪽 child Node를 가리킬 포인터 변수를 갖고있다.
class Node {
public:
int data;
Node* L, * R;
};BST Search
- 첫 시작 호출은 Search(root, X) 이다.
- Search(Node, X)는 원하는 값을 갖고있는 Node를 찾으면 그 노드의 주소를 반환하고, 없다면 nullptr을 반환한다.
- 나머지는 재귀적으로 구현된다.
- case 0 : 현제 Node가 null이라면 null을 반환한다.
- case 1 : 현재 Node의 key값이 X와 일치한다면 현재 Node의 주소를 반환
- case 2 : 현재 Node의 key값이 X보다 작다면, Search(Right child, X)를 재귀적으로 호출.
- case 3 : 현재 Node의 key값이 X보다 크다면, Search(Left child, X)를 재귀적으로 호출.
bool BST::Search(int x, Node** P, Node** D) {
*D = root;
*P = nullptr;
while (*D != nullptr) {
if ((*D)->data == x) { return true; } // case 1
else if ((*D)->data < x) { *P = *D; *D = (*D)->R; } // case 2
else { *P = *D; *D = (*D)->L; } // case 3
}
return false; // case 0
}▶ Search Correctness
To Prove : 만약 X가 한 노드의 key값과 같다면 Search(root, X)는 그 노드의 포인터를 반환할 것 이다. 아니라면 null을 반환할 것 이다.
이를 case 별로 증명해 보면 다음과 같다.
- case 0 : root가 null인 tree의 상황이다. node가 하나도 없으니 null을 반환함은 당연하다.
- case 1 : 이는 당연하다.
- case 2 : "현재 Node의 key값이 X보다 작다" 의 의미는 X는 Left subtree에는 들어갈수 없음을 의미한다. 따라서 X가 tree안에 있다면 이는 Right subtree안에 존재한다. 없다면 Search가 null을 재귀적으로 반환할 것 이다.
- case 3 : 역또한 성립
▶ 성능
트리가 한쪽 방향으로만 계속 연결되면 O(N)의 시간복잡도를 갖지만, 보통 O(logN)의 시간복잡도를 갖는다.
BST Insert
우선 Insert를 하기전에 삽입할 위치를 찾기위해서 Search를 수행해야 한다.
- Search 성공시 Insert() 는 실패한다. 값의 중복 오류
- Search 실패시 새로운 Node를 만들어 nullptr로 끝난곳에 삽입하면 된다.
bool BST::Insert(int x) {
Node* P, * D, * NN;
if (Search(x, &P, &D) == false) { // Search 실패시
NN = new Node;
NN->data = x;
NN->L = nullptr;
NN->R = nullptr;
if (P->data < x) P->R = NN;
else P->L = NN;
return true;
}
else
return false;
}증명 : "서브트리로 내려갔을 때, 만약 X가 트리에 존재한다면 그 곳에 있다"를 증명. 있다면 바로 실패처리되고 반복문을 반복하다 nullptr을 만나면 그곳에 insert를 해준다.
성능 : Search의 시간이 가장크다. 이후 노드의 추가는 O(1)안에 가능하다.
BST Delete
삭제 연산의 경우 총 3가지 경우로 나뉜다.
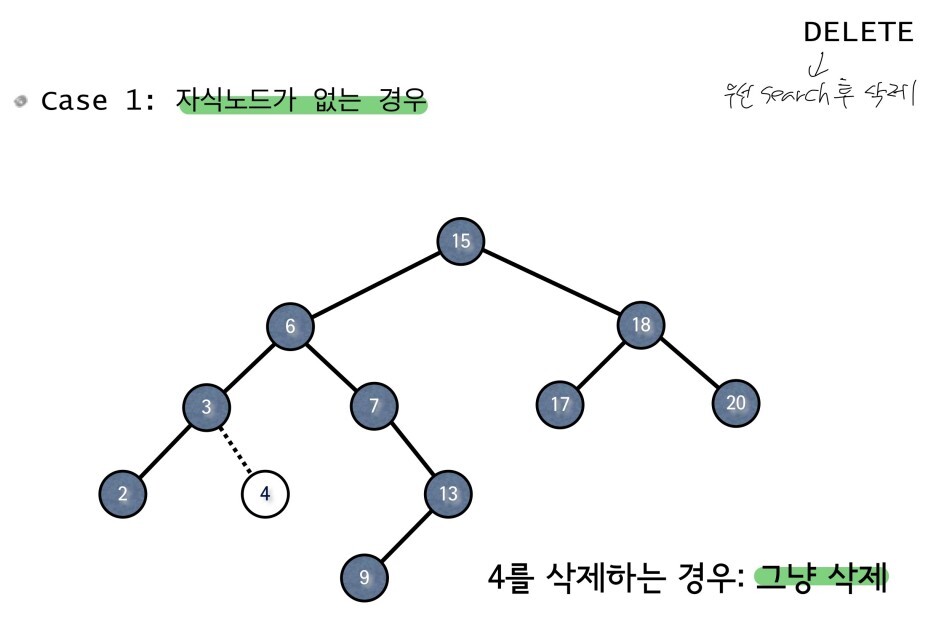
- case 1 : child가 없는 경우
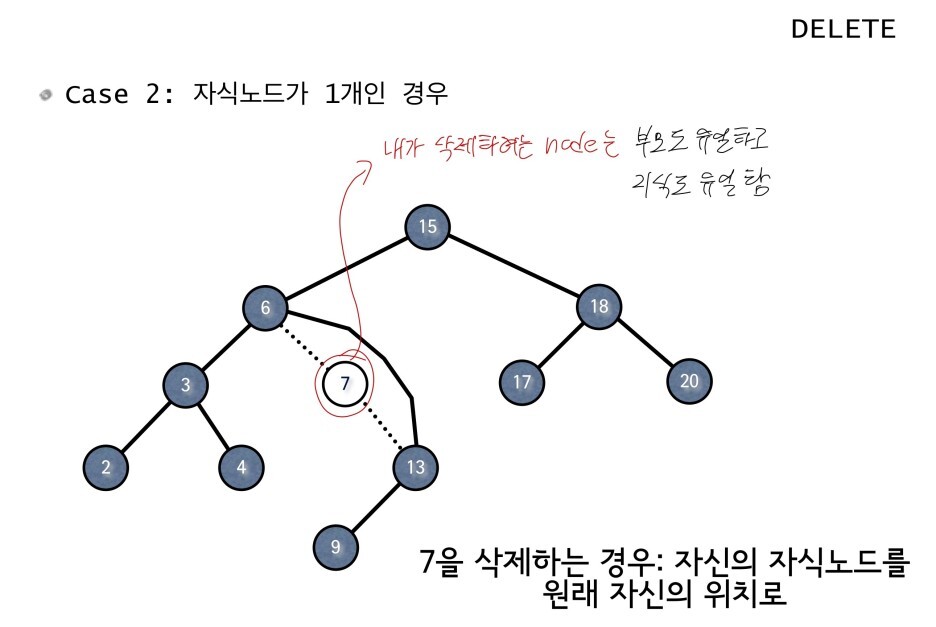
- case 2 : child가 하나 있는경우( 오른쪽 or 왼쪽 child )
- case 3 : child가 양쪽 모두 있는경우
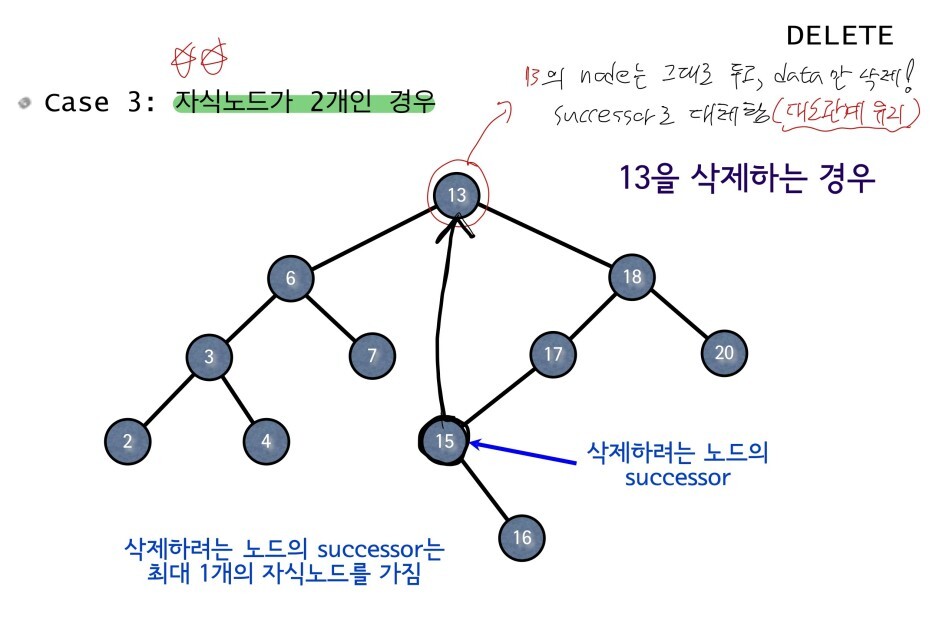

case 1과 2의 삭제 방식은 간단하지만, 3의 경우 많이 복잡해 진다.
bool BST::Delete(int x) {
Node* P, * D;
if (Search(x, &P, &D) == 1) {
if (D->L == nullptr && D->R == nullptr) {
if (D == P->L) P->L = nullptr;
else P->R = nullptr;
delete D;
}
else if (D->L == nullptr && D->R != nullptr) {
if (D == P->L) P->L = D->R;
else P->R = D->R;
delete D;
}
else if (D->L != nullptr && D->R == nullptr) {
if (D == P->L) P->L = D->L;
else P->R = D->L;
delete D;
}
else {
Node* RLL, *RLLP;
RLL = D->R; RLLP = D;
while (RLL->L != nullptr) {
RLLP = RLL;
RLL = RLL->L;
}
D->data = RLL->data;
if (RLL->L == nullptr && RLL->R == nullptr) {
if (RLL == RLLP->L) RLLP->L = nullptr;
else RLLP->R = nullptr;
delete RLL;
}
else if (RLL->L == nullptr && RLL->R != nullptr) {
if (RLL == RLLP->L) RLLP->L = RLL->R;
else RLLP->R = RLL->R;
delete RLL;
}
}
return true;
}
else return false;
}증명 : Lemma(보조정리)로서 "BST가 정의를 만족한다면 if and only if BST안에서 Search함수는 정확하게 작동한다" 를 활용한다.
만약 BST가 정확하지 않다면, 못찾는 값이 있다.
반대로
tree안에있는 모든 node에 대하여 Search가 성공한다면, BST는 정확하게 만들어진것 이다.
성능 : 정렬된 트리의 경우 height에 비례하게 된다. 이는 높은 확률로 O(logN)이다.
삭제와 관련된 글로 예전에도 정리해논 글이 있다 자세한 내용을 다음 링크를 통해 확인하길!
C++로 쉽게 풀어쓴 자료구조 : 9장, 이진 탐색 트리
내돈내고 내가 공부한것을 올리며, 중요한 단원은 저 자신도 곱씹어 볼겸 가겹게 포스팅 하겠습니다. 1) 9장. 이진 탐색 트리 이진 탐색 트리는 이진트리 기반의 탐색을 위한 자료구조로 효율적
blogshine.tistory.com
'CS > Data Structure (2021-1)' 카테고리의 다른 글
| [자료구조] 2-3-4 Tree, Red-Black Tree (2) | 2022.01.25 |
|---|---|
| [자료구조] AVL Tree, 2-3 Tree (0) | 2022.01.25 |
| [자료구조] Linked List (0) | 2022.01.25 |
| [자료구조] Equivalence Relation (0) | 2022.01.24 |
| [자료구조] Stack, Queue (0) | 2022.01.24 |

댓글