해당 본문은 학교수업시간에 배운 강의내용을 기반으로 정리하는 요약글 입니다. 정확하지 않은 점이 있으면 지적해주시면 감사하겠습니다.

이번 시간에는 AVL-Tree에 대하여 배웠다.
AVL-Tree 는 BST가 최악의 경우 linked-list 처럼 이어저 O(n)의 시간복잡도의 성능을 보여준다는 단점을 보완하는 tree이다.
AVL-Tree의 직관적 이해
다음 그림을 통해 AVL-Tree가 어떻게 보정 작업을 하는지 살펴보자.

왼쪽의 경우 root 노드인 6을 기준으로 왼쪽으로 node들이 치우쳐 있는 모습을 볼 수 있다. 이 tree의 H(높이)는 4에 해당한다.
이를 AVL-Tree의 정의에 부합하도록 보정 작업을 해주면 root가 바뀌면서 H가 3으로 변경이 가능해진다.
N개의 노드에 대해 AVL Tree는 O(logN)의 효율을 보인다. 가득 채우면서 내려가기 때문에 Height에 비해 노드 개수가 많다.
즉, tree에 새로운 Node를 Insert, Delete 할때 마다 보정 작업이 필요하게된다.
하지만 한가지 의문이 든다. 보정이 필요한 상황인지를 어떻게 파악할 것 인가?
정상과 비정상을 어떻게 빠르게 파악할 수 있을것 인가?
우선 AVL-Tree의 정의를 확인해 보자.
AVL-Tree Definition
AVL-Tree는 기본 BST(이진탐색트리)의 특성에 AVL의 추가조건이 추가된 것 이다. 이는 다음과 같다.
각 Node의 두가지 label 정보를 포함하게 되는데, 각각 L 과 R 이라 부른다.
L : Height of Left subtree / R : Height of Right subtree
Condition : L-R의 절댓값이 2 미만이어야 한다. 즉, L-R은 -1,0,1 중 하나이어야 한다.
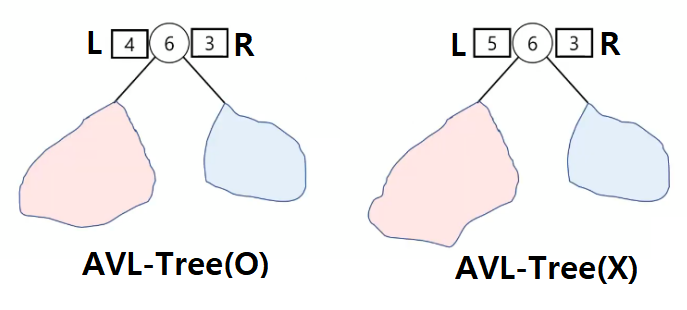
위의 그림을 통해 확인해볼 수 있다. L에는 left subtree의 높이가, R에는 right subtree의 높이가 저장되 있다.
오른쪽의 경우에는 이 수치의 차이가 2가 나기때문에 AVL-Tree의 조건에 부합하지 않는다.
AVL-Tree의 Height Bound?
AVL-Tree의 높이는 노드의 수가 N개 일때 O(logN)에 해당한다고 한다. 이를 어떻게 증명할 것 인가??
이를 위해 몇가지 정의가 필요하다.
1) Down Sequence Definition
- 문자 L과 R은 노드에서 child 내려갈때 내려갈 방향을 의미한다. 예를들어 LLRLR은 왼쪽-왼쪽-오른쪽-왼쪽-오른쪽 으로 진행하는 것 이다.
- Root로부터 시작해서 내려간다.
- 몇몇 Down Sequence는 끝까지 수행될 수없다. 예를 들어 LLRLR이라는 순서가 있는데, tree의높이가 3 이라면 4부터는 더이상 child가 없어 끝까지 이 순서가 진행되지 못하고 끝날 것 이다. 다음 그림처럼 말이다.

2) Terminated Down Sequence
- Terminated Down Sequence는 바로 직전 그림에서 빨간 박스안 문자열을 의미한다. 마지막 문자인 R의 경우 이동이 불가능한 지점으로써 빨간색으로 표시해준다. L L R 처럼 말이다.
이를 바탕으로 AVL-Tree의 모든 가능한 Terminated Down Sequence를 구해보자.

< Observation >
1) 가장 긴 Terminated Down Sequence는 가장 짧은 Terminated Down Sequence의 약 2배이다.
이를 어떻게 이해할 수 있을까? 우선 조금 직관적으로 접근해 보자.
longest down sequence를 따라서 내려가면서 label을 확인해 보면 k, k-1, k-2, ... , 3, 2, 1, 0 으로 끝난다.
label간의 간격이 1인 상황이다. 항상 긴쪽으로 내려가야 하니 1씩 차이가 나는 것 이다.
길이를 2L이라 할수 있다.
shortest down sequence를 따라서 내려가면서 label을 확인해 보면 k-1, k-3, k-5, ... , 4, 2, 0 으로 끝난다.
label의 간격이 2씩 나는 상황이다. 항상 짧은 쪽으로 내려가야하니 2씩 차이 나는 것 이다. 직전 그림에서도 확인이 가능하다
길이를 2L의 절반인 L이라 할 수 있다.
즉 다음 그림에서 확인 가능 하듯 가장 짧은 길이는 logN이고 가장 긴 길이는 2logN이다.

2) 가장 짧은 Terminated Down Sequence 위에는 모든 Node가 가득 차있다.
이는 직전의 그림에서 파란색 글씨를 확인해 보면 직관적으로 이해할 수 있다.
3) 엄밀한 계산
root의 레이블 L/R 중에서 큰 것이 K라면, height는 K+1이된다.
가장 짧은 Down Sequnce의 길이는 최소 K/2이며, 가장 짧은 순서의 leaf node 위 레벨들은 노드로 가득 차있다.
(해당 레벨 위까지의 노드 개수 2^(k/2)개)
가장 짧은 leaf 노드가 약 K/2라고 하면 노드 개수는 최소 2^(k/2)개이며 가장 긴 경우 길이가 K이니 최대 2^(K)개 이다.
따라서 노드개수 N을 기반으로 부등식을 구해보면,
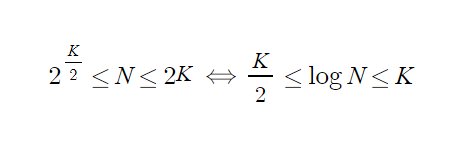
즉 height는 O(logN)이 되고, AVL-Tree에서의 search도 O(logN)이 된다.
BUT...
insert와 delete 사용시 AVL-Tree는 label L/R에 대한 정의가 깨질 수 있다. 이를 주의해야 한다.
AVL-Tree Insert
- Insert만을 고려해 보자. Delete의 경우 거의 유사하다.
- Algorithm
1) 일반 insert를 수행한다. 삽입시 새로운 Node는 leaf-node에 삽입된다.
2) 삽입 후, leaf-node에서부터 tree를 거꾸로 올라가면서 label값을 수정한다. 1씩 증가될 것 이다.
3) 조건이 처음으로 만족되지 않는 Node에서 rotation을 수행한다.
4) 끝 (한 Node에서 rotation이 수행된 후, 그 위의 노드들은 보정이 필요없어진다.)
다음 그림은 맨 처음 조건이 만족되지 않는 Node의 상황이다.

AVL-Tree Rotation
Rotation은 새로운 node가 추가된 위치에 따라 달라진다.
조건 불만족이 발생한 노드 기준 새로운 노드가 추가된 위치가 LL(Left,Left)방향인지, LR(Left,Right)인지, RL(Right,Left)인지, RR(Right,Right)인지에 따라 Rotation 방식이 달라진다.
케이스 별 상황은 다음 블로그 글을 살펴보자
- 각 Node는 1개 또는 2개의 key값을 갖는다.
- 각 Node는 최대 3개의 child를 갖을 수 있다.
- 각 Node들은 chlid를 1개만 갖을수는 없다. 아예 없거나 or 2,3개의 child를 갖어야 한다.

- Root에서 모든 leaf노드 까지의 거리가 같다.
- 노드의 수가 N일때 2-3 Tree의 높이는 O(logN)이다. 이를 직관적으로 이해하여 보자.
높이가 3일때 최소 개수의 key는 몇개 인가? 최대는 몇개인가?
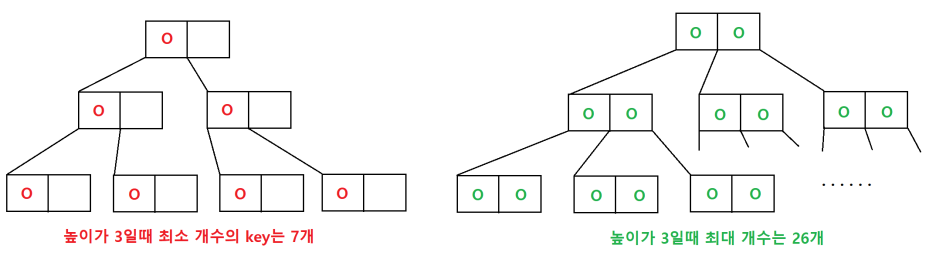
즉 min N = 2^h-1 이고, max N = 3^h-1 이다.
이를 양변에 log를 취하면 다음과 같아진다.

이는 O(logN)에 해당하게 된다.
2-3 Tree Insert
1) Root에서 시작해서 Leaf까지 쭉 내려가면서 Search를 진행한다.
2) Leaf가 1개 혹은 2개의 key값을 갖는지 확인한다.
- case 1 (1개의 key) : 빈자리 있는 경우다. 그냥 삽입하고 끝난다.
- case 2 (2개의 key) : 빈자리가 없는 경우다. 해당 leaf node를 둘로 나눈후, 중간값을 parent node로 올려 보낸다.
2 3 - 2
/ insert 3 / \
1 - 4 ----> 1 4
3) 2번에서 parent로 값을 하나 올린경우
- case 1 (1개의 key) : 빈자리 있는 경우다. 그냥 삽입하고 끝난다.
- case 2 (2개의 key) : 2개로 나눈후 다시 또 위로 값을 올린다.
4) 계속 올리다가 parent가 없는 경우 새로운 root를 만든다.
2-3 Tree는 모든 leaf가 동일한 level에 있어야 하기 때문에 아래쪽에 추가하는 것 이 아닌, 좌우 로 넓혀가는 방식이다.
이런식으로 하면 모든 leaf가 같은 level에 있음이 보장된다.
'CS > Data Structure (2021-1)' 카테고리의 다른 글
| [자료구조] Priority Queue, Dijkstra (0) | 2022.01.25 |
|---|---|
| [자료구조] 2-3-4 Tree, Red-Black Tree (2) | 2022.01.25 |
| [자료구조] Binary Search Tree (0) | 2022.01.25 |
| [자료구조] Linked List (0) | 2022.01.25 |
| [자료구조] Equivalence Relation (0) | 2022.01.24 |

댓글