
이번 장에서는 소수와 실수의 표현과 그 연산과정에 대하여 학습하는 시간이다.
기본적인 덧셈과 뺄샘의 정리는 생략
3.3 곱셈
우선 연필로 곱셈하는 과정을 살펴보자. 0과 1로만 구성된 십진수의 곱셈을 살펴보자.
1000(ten) 곱하기 1001(ten)은 다음과 같다.

첫 번째 피연산자는 피승수(multiplicand)라고 부르고 두 번째 피연산자는 승수(multiplier)라고 부른다.
최종 결과는 곱(product)라고 부른다.
일반적으로 수학에서 우리가 곱셈을 할때 승수의 자릿수를 오른쪽에서 왼쪽으로 가면서 한 번에 하나씩 택해서 이것을 피승수와 곱한 뒤 그 곱셈의 결과를 직전의 곱보다 한 자리 왼쪽에 놓는다.
주목할 점은 최종 곱셈 결과의 자릿수가 피승수나 승수와 비교해서 상당히 크다는 것 이다.
사실 부호 비트를 무시한다면 n비트의 피승수에 대한 m비트 승수의 곱셈 결과는 n + m 비트의 길이를 갖는다. 결국 모든 가능한 곱을 표현하기 위해서는 n + m비트가 필요하다.
따라서 이는 오버플로우 문제가 도사리는데, 두 32비트 수의 곱셈 결과가 32비트가 되기를 바라는 경우가 많기 때문이다.
3.3.1) 곱셈 알고리즘과 하드웨어의 순차적 버전
▶ version 1
첫 번째 설계는 직전에 본 일반적인 수학에서 배운 곱셈 알고리즘과 유사하다. 다음 필요한 하드웨어를 살펴보자.
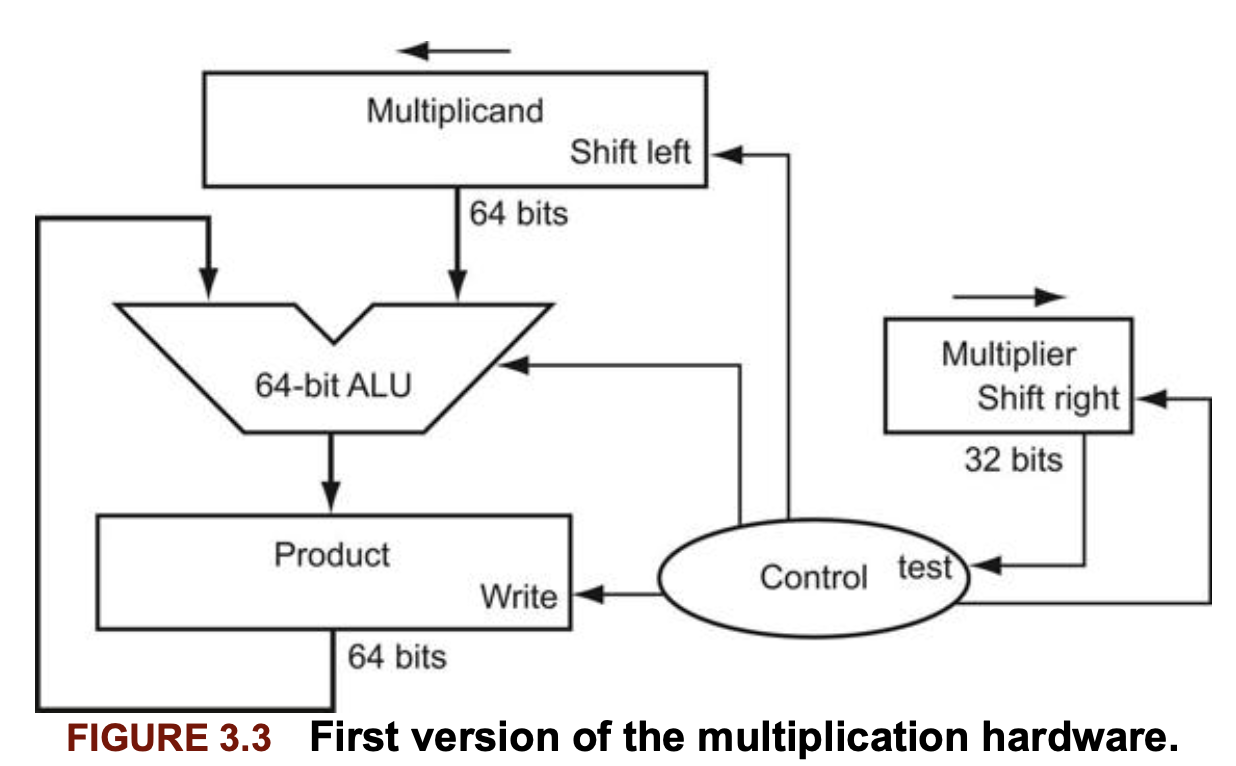
Multiplicand(피승수) 레지스터, ALU, Product 레지스터는 모두 64bit이고, Multiplier(승수) 레지스터만 32비트 이다.
시작할 때는 32비트 피승수가 피승수 레지스터 오른쪽 절반에 있다가 매 단계마다 왼쪽으로 1비트 씩 자리 이동된다. 승수는 매 단계마다 반대 방향으로 자리이동된다. 알고리즘은 곱 레지스터를 0으로 초기화하고 시작된다. control은 피승수 레지스터와 승수 레지스터를 언제 자리이동할지, 또 새로운 값을 언제 곱 레지스터에 쓸지를 결정한다.
매 단계마다 피승수를 왼쪽으로 한 자리씩 이동시키고 필요하면 중간 결과에 더해 주는 식으로 계산 되어야 함을 알 수 있다.
이렇게 32비트 피승수로, 왼쪽 절반은 0으로 초기화 된다. 이 레지스터는 64비트 곱 레지스터에 축적되는 합과 피승수의 위치를 맞추기 위해서 매 단계마다 1비트씩 왼쪽으로 자리이동 한다.
다음 그림3.4는 전체적인 알고리즘을 보여준다.
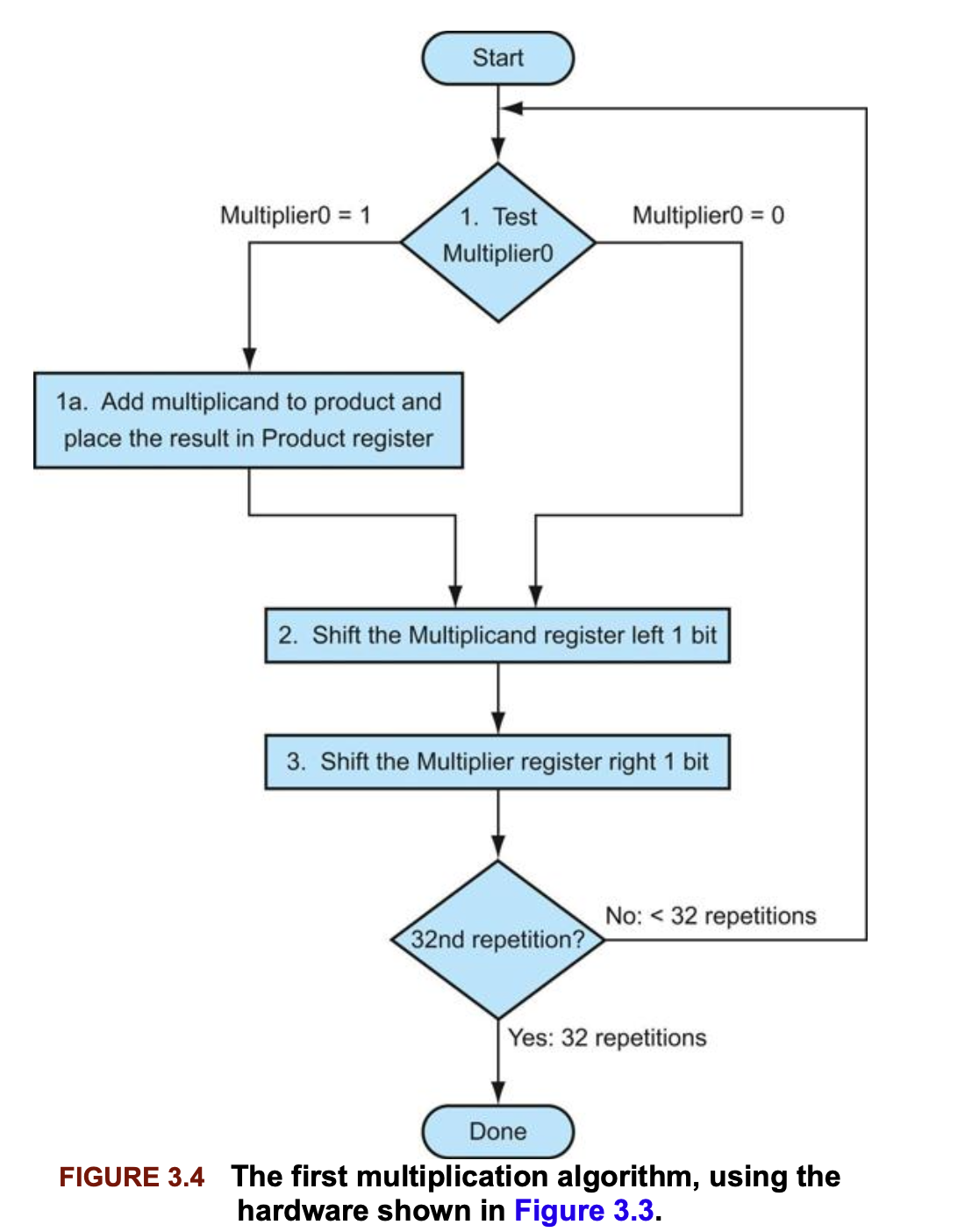
중요한 점은 승수의 최하위 비트(Multiplier0)는 피승수를 곱 레지스터에 더할지 말지를 결정한다.
승수의 최하위 비트가 1이면 피승수를 곱에 더한다. 그렇지 않으면 다음 단계로 진행한다.
최종 결과를 얻기 위해서는 이 과정을 32번 반복한다.
▶ ver2
좀더 개선된 버전을 살펴보자. ver2 같은 경우 multiplicand 레지스터는 32비트로 고정해두고, product의 자리를 오른쪽으로 한칸씩 이동시킨다.
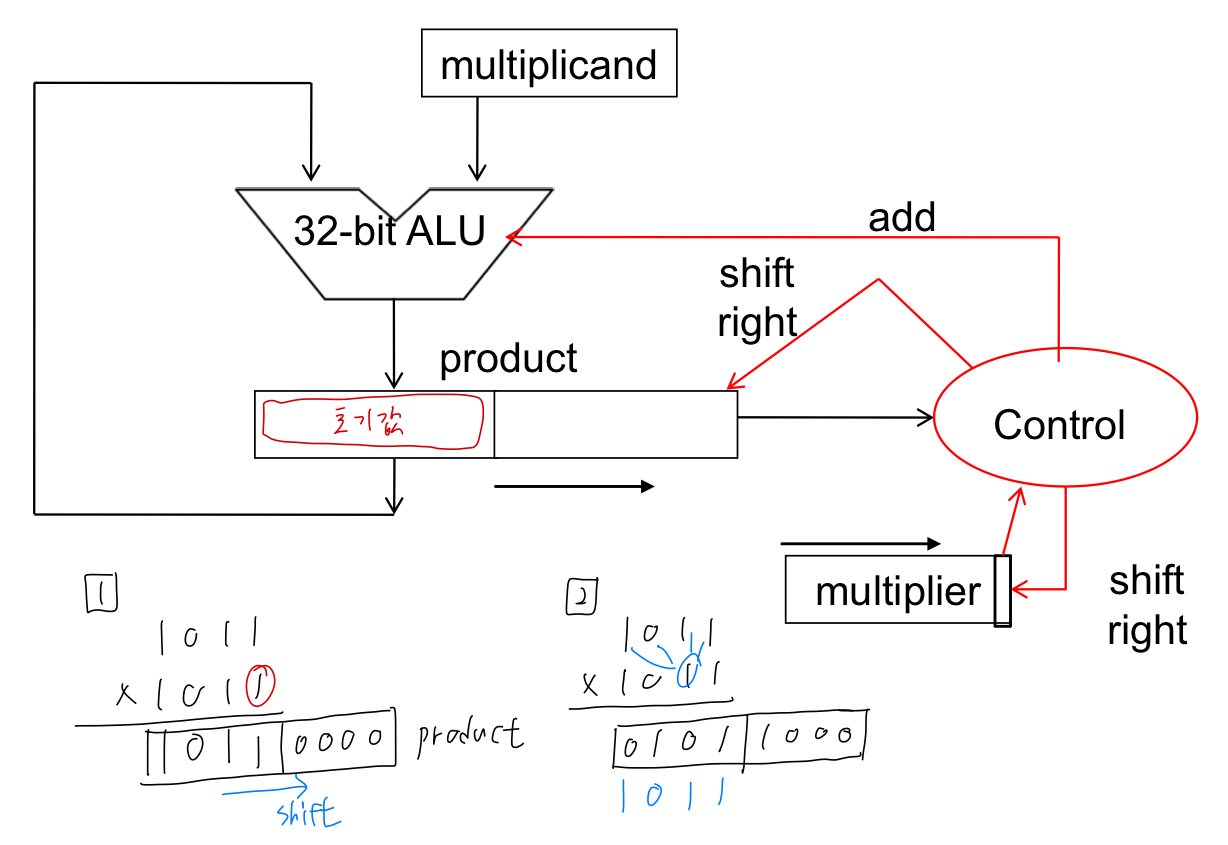
곱하기 1011 x 1011을 생각해보면 위와 같다.
피승수를 고정한 상태에서 승수의 첫 비트값인 "1"을 확인하면 피승수의 "1011"을 product의 왼쪽 32비트에 저장한다.
이후 product와 multiplier 모두 오른쪽으로 1칸 shift한다.
다시 multiplier 첫 비트값을 보면 "0"이다. 이번에는 "0000"을 product의 최상위 32비트에 더해준다.
이후 product와 multiplier 모두 오른쪽으로 1칸 shift한다.
이를 반복한다.
▶ ver3
마지막 버전을 살펴보자!
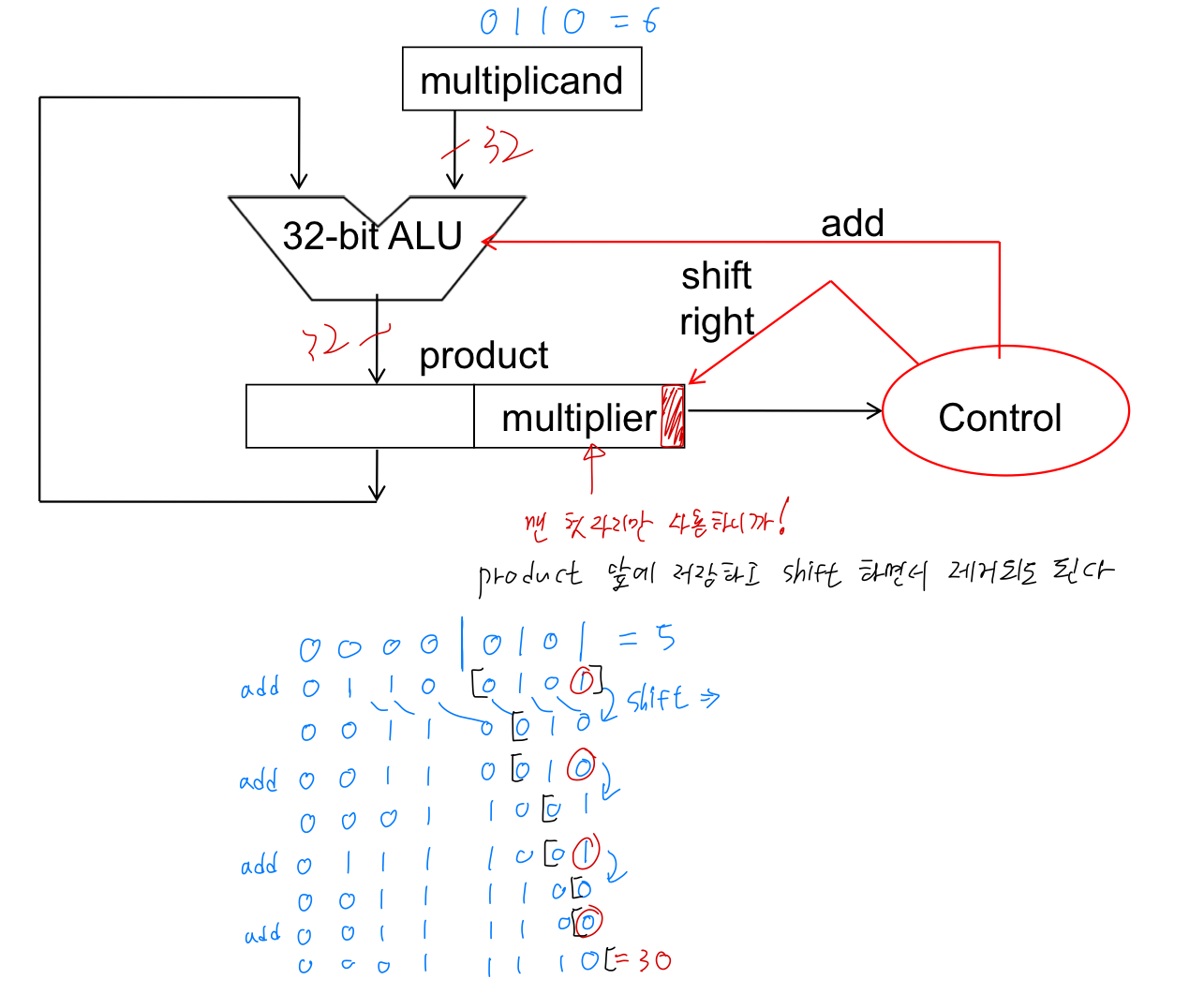
0110 x 0101을 수행한 결과이다. 이전과 달리 multiplier 레지스터를 따로 두는 것 이 아니라, product의 오른쪽 32비트에 초기화 시켜둔다.
이는 매 연산마다 오른쪽으로 1비트씩 product를 이동시켜 최 하위 비트의 0, 1 유무에 따라 multiplicand를 product의 상위 32비트에 더하는 방식으로 진행된다.
최종적으로 32번의 연산이 끝나면 자연스럽게 multiplier는 product에서 사라지고, 최 하위 32비트에는 곱셈의 결과만이 남게 된다!
3.3.2) 부호있는 곱셈
지금까지는 양수만 다루었다. 부호있는 수의 곱셈을 가장 쉽게 이해할 수 있는 방법은 먼저 승수와 피승수를 양수로 변환하고 원래 부호를 기억하는 것 이다. 이 알고리즘은 부호를 계산에서 제외시키고 31번 반복한 후, 초등학교에서 배운 대로 피 연산자들의 부호가 서로 다를 때만 곱을 음수로 바꾼다.
3.4 나눗셈
곱셈의 역 연산인 나눗셈은 사용 빈도는 낮은 반면 훨씬 까다롭다. 심지어는 0으로 나누기와 같은 수학적으로 유효하지 않은 연산을 하는 경우도 생긴다.
예시를 하나 살펴보자, 1,001,010(ten) 나누기 1000(ten)이다.
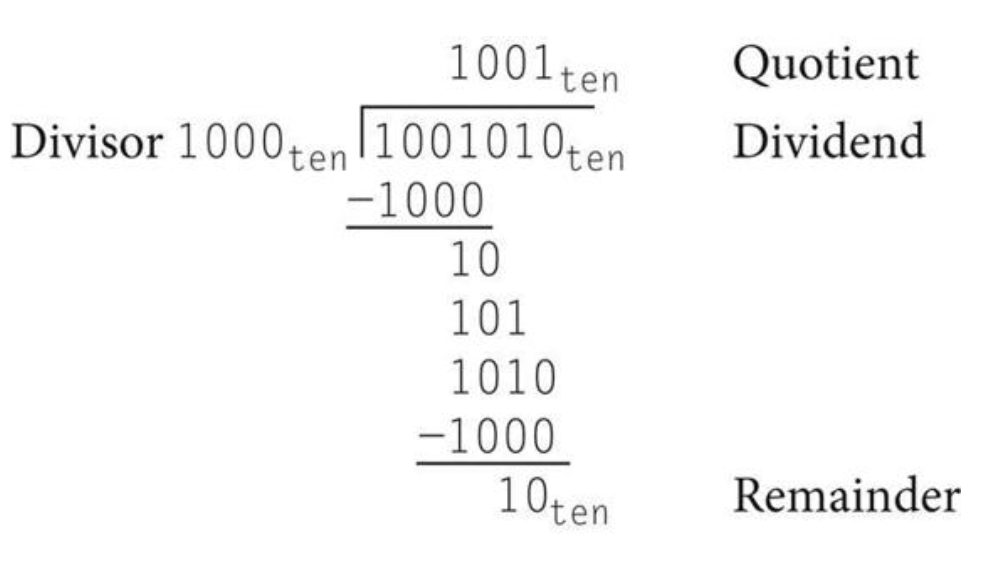
나눗셈의 피연산자는 피제수(dividend)와 제수(divisor) 두개이고, 몫(quotient)이라 불리는 결과와 나머지(remainder)라고 불리는 두 번째 결과가 있다.
피제수 = 몫 x 제수 + 나머지위의 10진수 예는 0과 1만을 사용하도록 매우 조심해서 선택하였으므로, 제수가 피제수에 얼마나 많이 들어갈 수 있는지를 쉽게 알 수 있다.
0번 아니면 1번이다.
3.4.1) 나눗셈 알고리즘과 하드웨어
▶ version 1
다음 그림은 초등학교에서 배운 알고리즘을 그대로 하드웨어로 구현한 것 이다. 몫 레지스터 32비트를 0으로 초기화시키고 시작한다.
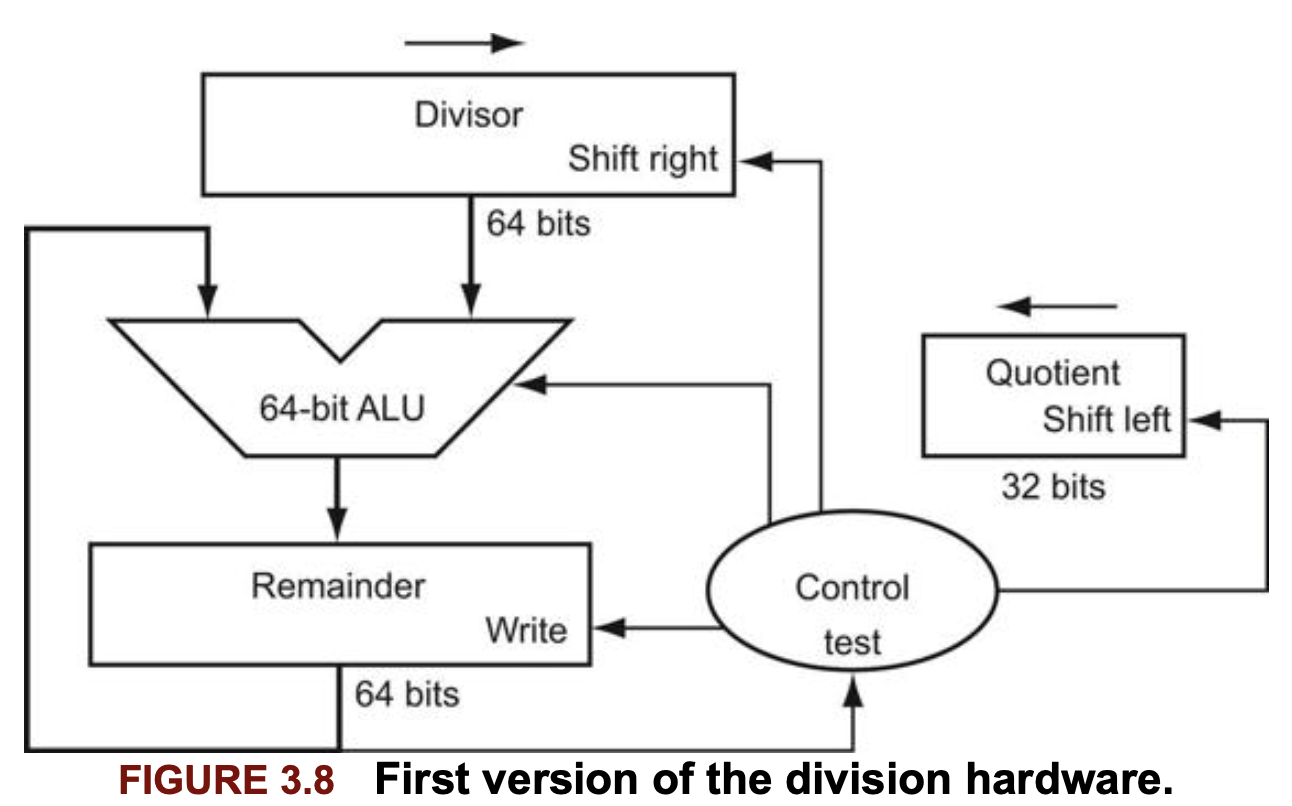
이 알고리즘은 매 반복마다 제수(divisor)를 오른쪽으로 한 비트씩 자리이동해야 하므로 제수를 64비트 제수 레지스터의 왼쪽 절반에 넣고 시작한다. 그리고 피제수와 자리를 맞추기 위해 반복할 때마다 오른쪽으로 한 비트씩 자리이동한다. remainder 레지스터는 피제수(dividend)로 초기화 된다.
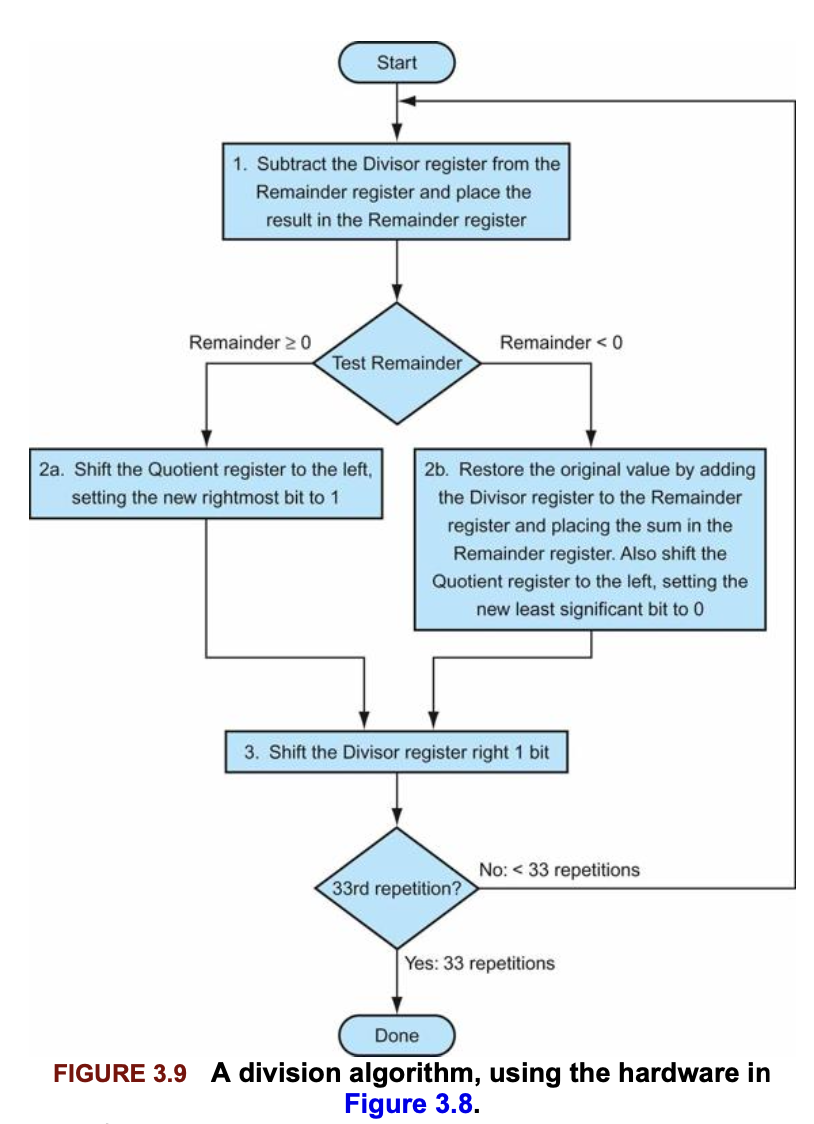
컴퓨터는 사람과 달리 제수가 피제수보다 작다는것을 알지 못한다. 따라서 1단계 에서 먼저 (피제수 - 제수)를 뺴는 연산을 수행해야 한다.
이는 set on less than 명령어에서 했던 비교와 같다.
만약 결과가 양수면 -> (제수 <= 피제수) -> 몫에 1을 삽입한다. (위 그림 2a)
만약 결과가 음수면 -> (제수 > 피제수) -> 제수를 나머지 레지스터에 다시 더함으로써 원래의 값을 회복하고 몫에는 0을 삽입한다.
제수는 오른쪽으로 한칸 이동하고, 이 과정을 반복한다.
▶ version 2
레지스터와 덧셈기에 사용되지 않는 부분이 있음을 활용하여 레지스터의 크기를 절반으로 줄일수 있다.
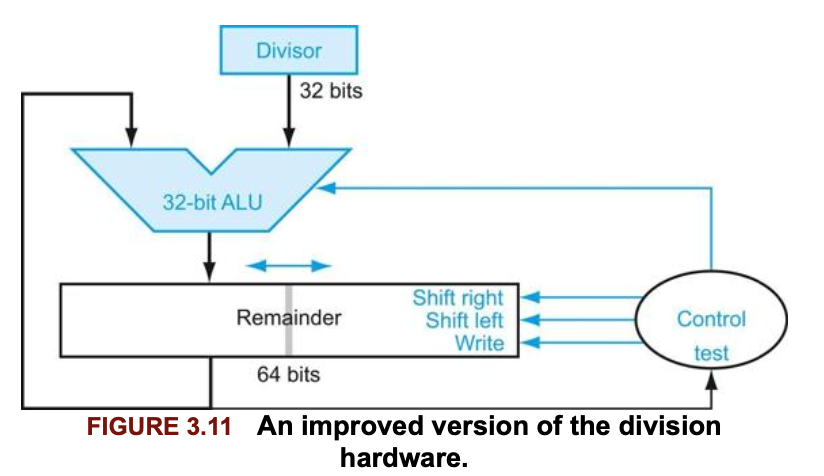
이전 버전과 다른점은, divisor는 움직이지 않고, remainer를 왼쪽으로 이동시키면서 사용하는 것 이다.
이전과 달리 divisor, ALU, 몫 레지스터가 32비트로 반으로 줄어들었다.
예를 들어 7 나누기 2를 한다고 생각해보다.
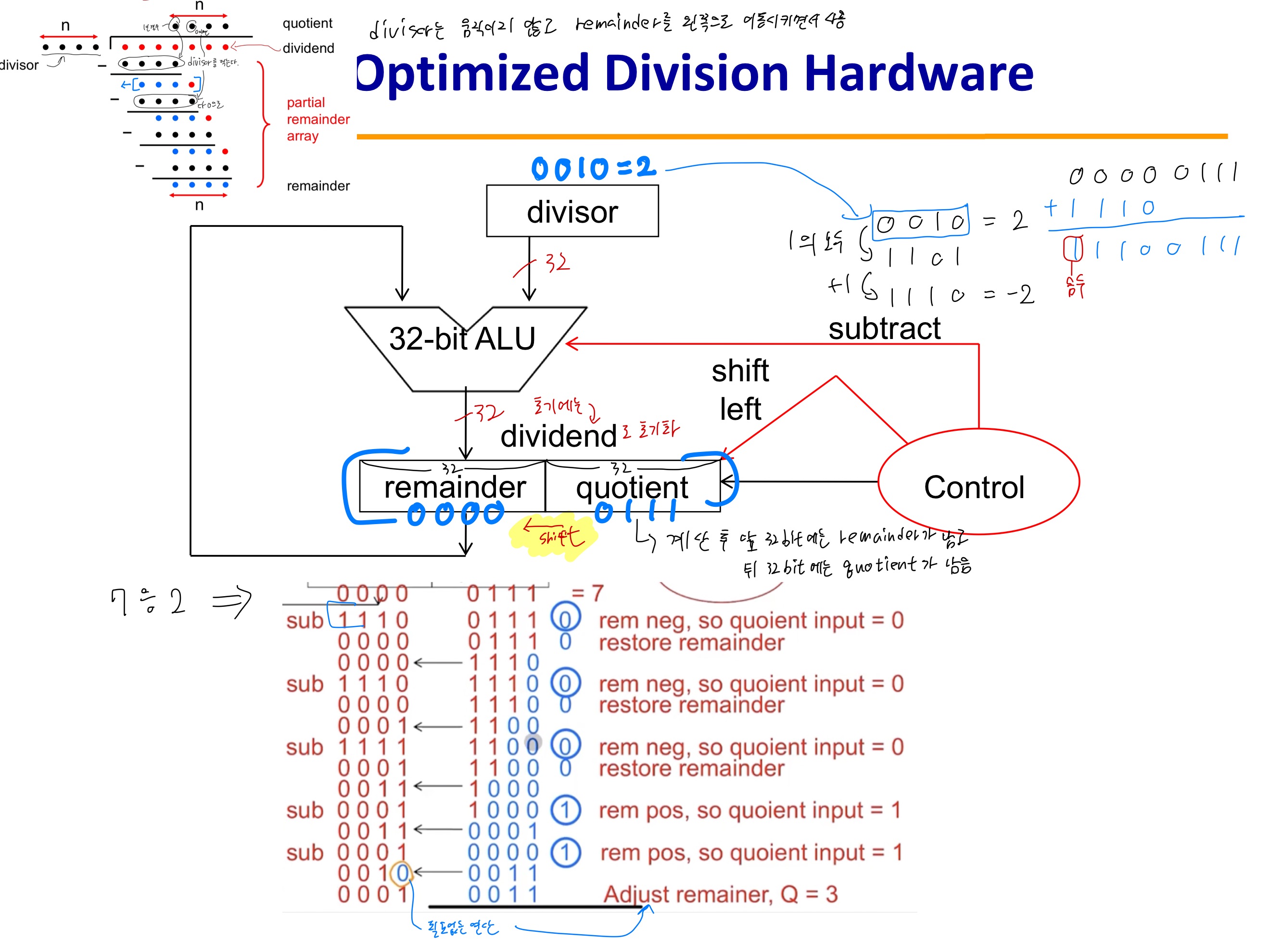
1) 초기에 divisor에는 제수인 2를 2진수 0010으로 삽입해준다.
2) 64비트 remainder 레지스터의 최상위 32비트를 제수 7(0000 0111)로 초기화 하고, 하위 32비트는 모두 0으로 초기화 한다
3) remainder 상위 32비트(제수)에서 divisor를 뺀다. -> 빼기 결과가 양수이므로 quotient하위 32비트에 1을 추가해준다.
4) Remainder 레지스터 전체의 값을 왼쪽으로 한칸 이동시킨다
5) 이를 반복한다.
이렇게 나머지를 계속 반복하고 나면, 최종적으로 remainder레지스터 하위 32비트에는 몫만 남게된다.
3.5 부동 소수점
프로그래밍 에서는 정수 뿐만 아니라, 소수 부분을 갖는 수도 다를 수 있다. 수학에서는 이런 수를 실수(real)라 부른다.
정규화된 수(normalized number)는 소수점의 왼쪽에는 한 자릿수만 있다.
과학적 표기법으로 표현된 숫자 중에서 맨 앞에 0이 나오지 않는 것을 정규화된 수라고 부른다.
예를들어 1.0 * 10^-9는 정규화된 수 이지만, 0.1 * 10^-8은 아니다.
이진수를 정규화된 수로 나타내면 다음과 같다.
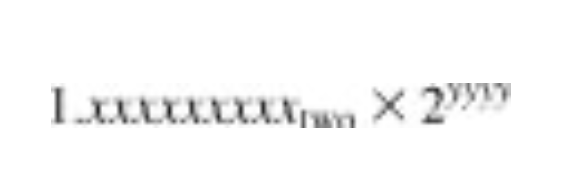
실수를 정규화된 형태의 형태의 표준 과학적 표기법으로 나타내면 3가지 장점이 있다.
1) 부동 소수점 숫자를 포함한 자료의 교환을 간단하게 한다
2) 숫자가 항상 이런 형태로 표현된다는 것을 알고 있으므로 부동 소수점 알고리즘이 간단해진다.
3) 불필요하게 선행되는 0을 소수점 오른쪽에 있는 실제의 숫자로 바꾸기 때문에 한 워드 내에 저장할 수 있는 수의 정밀도를 증가시킨다.
3.5.1) 부동 소수점 표현
부동 소수점 표현 방식을 설계하는 사람은 소수 부분(fraction)의 크기와 지수(exponent)의 크기 사이에서 타협점을 찾아야 한다.
왜냐하면 고정된 워드 크기를 사용하므로 한쪽을 증가시키면 당연히 다른쪽의 크기가 줄어든다.
이 문제는 정밀도와 표현 범위 사이의 선택이다.
부동 소수점의 크기는 보통 워드 크기의 배수이다. MIPS의 부동 소수점 표현은 아래 그림과 같다.
여기서 s는 부호부분, 지수는 8비트, 소수 부분은 23비트의 수 이다. 이를 부호화 크기(sign and magnitude) 표현 방식이라 부른다.

일반적으로 부동 소수점 수는 다음과 같은 형태를 갖는다.
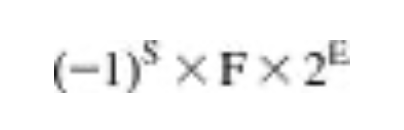
따라서 2.0 * 10^-38 부터 2.0 * 10^38만큼 큰 수가 컴퓨터에서 표현될 수 있다.
하지만 이는 무한대가 아니기 때문에 이보다 더 큰 계산 결과가 나올수 있다. 따라서 부동 소수점 연산에서도 오버플로(overflow)가 발생할 수 있다.
또한 너무 작아서 표현할 수 없는 경우 언더플로(underflow)라 부른다. 이는 음수 지수의 절대값이 너무 커서 지수 부분에 표현될 수 없는 경우를 말한다.
언더플로우의 발생 가능성을 줄이는 방법으로 지수 부분이 더 큰 다른 자료형을 사용할 수 있다. C언어 에서는 이를 double이라 부른다.
이를 2배 정밀도(double precision) 부동 소수점 연산이라 부른다. 앞서 설명한 표현 형식은 단일 정밀도(single precision)이라 부른다.
2배 정밀도 부동소수점의 수를 표현하려면 다음과 같이 MIPS 워드 2개가 필요하다
여기에서 s는 여전히 수의 부호를 나타내고, 지수는 11비트의 지수 필드 값을, 소수부분은 52비트이다.

2배 정밀도의 경우 훨씬 더 큰 유효자리를 제공하여 정밀도를 높인다는 것 이다.
이것들은 IEEE 754 부동 소수점 표준 으로, 1980년 이후에 만들어진 컴퓨터는 거의 모두 이 표준을 사용하고 있다.
유효자리 부분에서 더 많은 수를 표현하기위해 IEEE 754 표준은 정규화된 이진수의 가장 앞쪽 1비트를 생략하고 표현하지 않는다.
따라서 실제적으로 유효자리는 단일 정밀도 표현에서는 24비트의 길이를 갖는다.(숨겨진 1 + 23비트)
표현을 정확하기 하기 위해서, 유효자리(significand)라는 용어는 숨겨진 1을 포함하는 24 또는 53비트를 나타내는데 사용하고, 원래의 23비트는 소수 부분이라 부른다.
다만 예외적으로 0은 00...00(two)를 예약하여 사용한다.
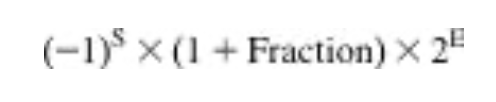
IEEE754의 설계자들은 정수 비교에 의해서 쉽게 sorting될 수 있는 부동 소수점 표현을 원했다.
이러한 이유로 less then, greater than, 또는 equal to 0 테스트를 빠르게 할 수 있도록 부호 비트가 최상위 비트에 놓이게 되었다.
지수를 유효자리 앞에 두면 부호가 같은 수를 비교할 때 지수가 큰 수가 지수가 작은 수보다 더 큰 정수처럼 보인다.
하지만 음수를 비교할때 지수는 숫자 정렬을 어렵게 만든다. 만약 음의 지수를 나타내기 위해 2의 보수법이나 지수의 최상위 비트는 1로 만드는 어떤 표현법을 상요한다면, 지수가 음수이면 매우 큰수처럼 보일 수 있다.


위의 두 표현의 지수부를 보면 음수가 더 큰것처럼 보인다.
따라서 가장 음수인 지수를 00...00(two)로, 가장 양수인 지수를 11...11(two)로 표현하는 것 이다.
이와같은 방식을 biased notation이라 부릅니다.
IEEE754의 단일 정밀도 표현 방식에서는 바이어스 갑으로 127을 사용한다. 2배 정밀도는 1023이다.
따라서 -1은 -1 + 127 = 126 즉, 0111 1110(2진수)라는 비트 패턴으로 표현된다.
그리고 +1은 +1 + 127 = 128 즉, 1000 0000(2진수)라는 비트 패턴으로 표현된다.
3.6 부동 소수점 덧셈
부동 소수점으로 표현된 수들의 덧셈을 이해하기 위해 먼저 과학적 표기법으로 표시된 두 수 9.999 x 10^1 과 1.610 x 10^-1을 손으로 더해보자. 유효자리에 4자리 그리고 지수에 2자리의 십진수를 저장할 수 있다고 가정한다.
▶ 단계 1
두수를 더하기 위해서는 먼저 작은 지수를 갖는 수의 소수점을 정렬해야 한다.
따라서 작은 수 1.610 x 10^-1을 큰 지수와 일치하는 형태로 바꾸어야 한다.
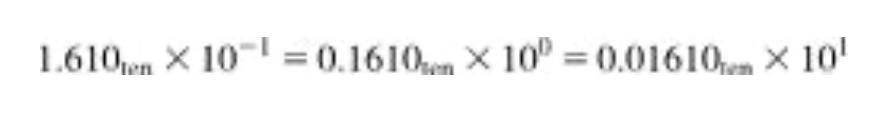
위에서 가장 오른쪽의 형태가 우리가 필요한 형태이다.
그러나 우리는 4자리의 십진수만을 표시할 수 있기 때문에 자리이동한 후의 수는 다음과 같다.
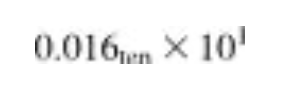
▶ 단계 2
유효자리를 서로 더한다.
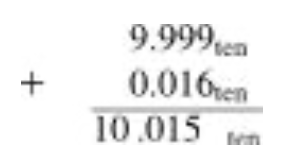
합은 10.015 x 10^1이 된다.
▶ 단계 3
이 합은 정규화된 과학적 표기법이 아니므로 정리를 좀 해줘야 한다.
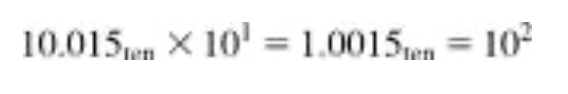
▶ 단계 4
유효자리가 4자리 라고 가정했기 때문에(부호 제외) 수를 rounding해줘야 한다. 이때 반올림을 사용하자
따라서 반올림을 하면 다음과 같다.
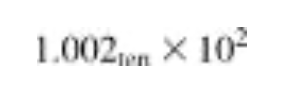
다음 플로우 차트는 이진수 부동 소수점 덧셈 알고리즘을 보여준다.
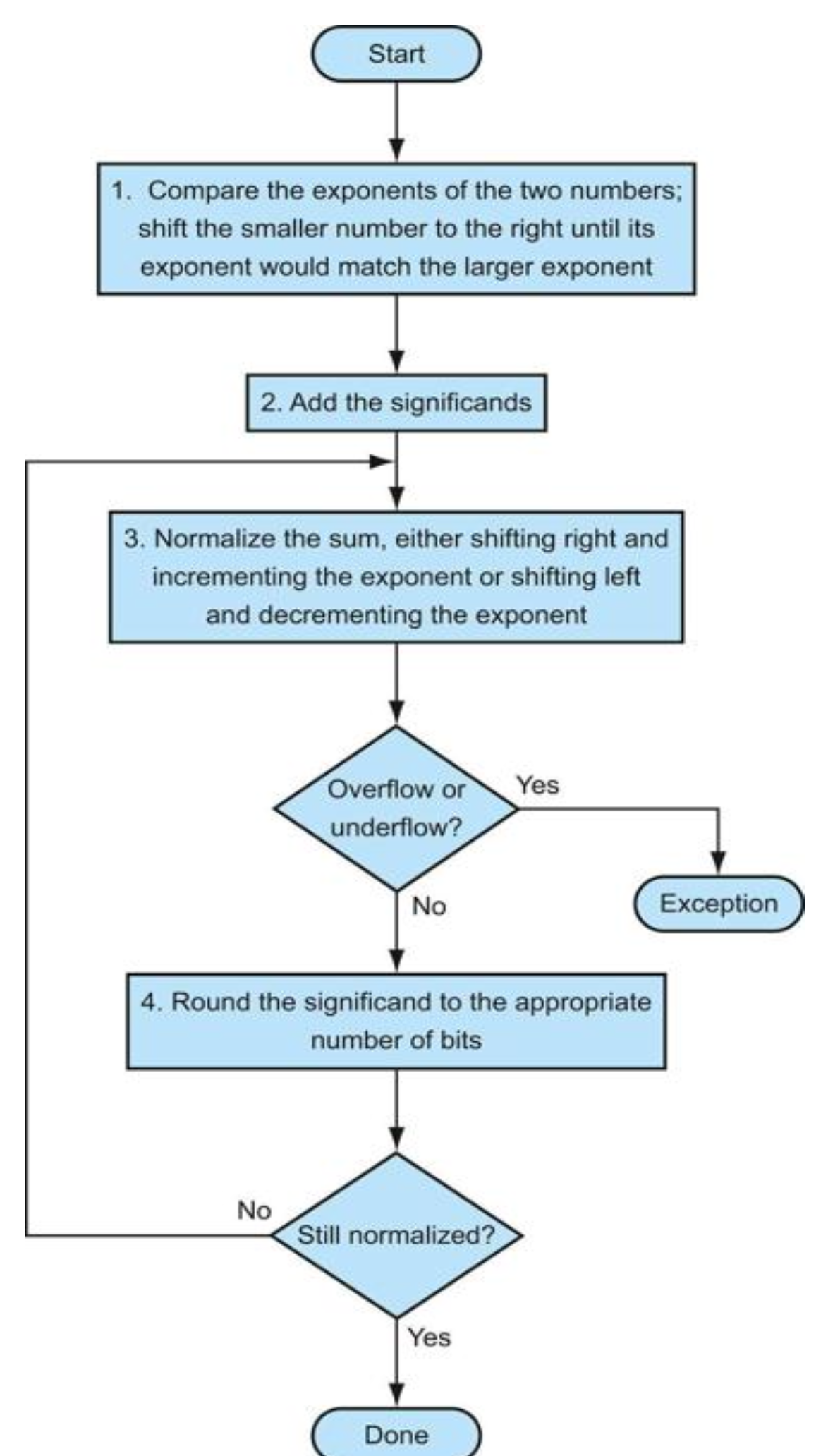
단계 1, 2는 앞의 예제와 같다. 작은 지수를 갖는 수의 유효자리를 조정한 후 두 유효자리 수를 더한다.
단계 3은 오버플로와 언더플로를 검사하면서 결과를 정규화 한다.
부동 소수점 계산을 빠르게 하기 위해 전용 하드웨어를 사용하는 컴퓨터가 많이있다. 다음은 소숫점 덧셈을 위한 하드웨어의 기본 구조를 보여준다.
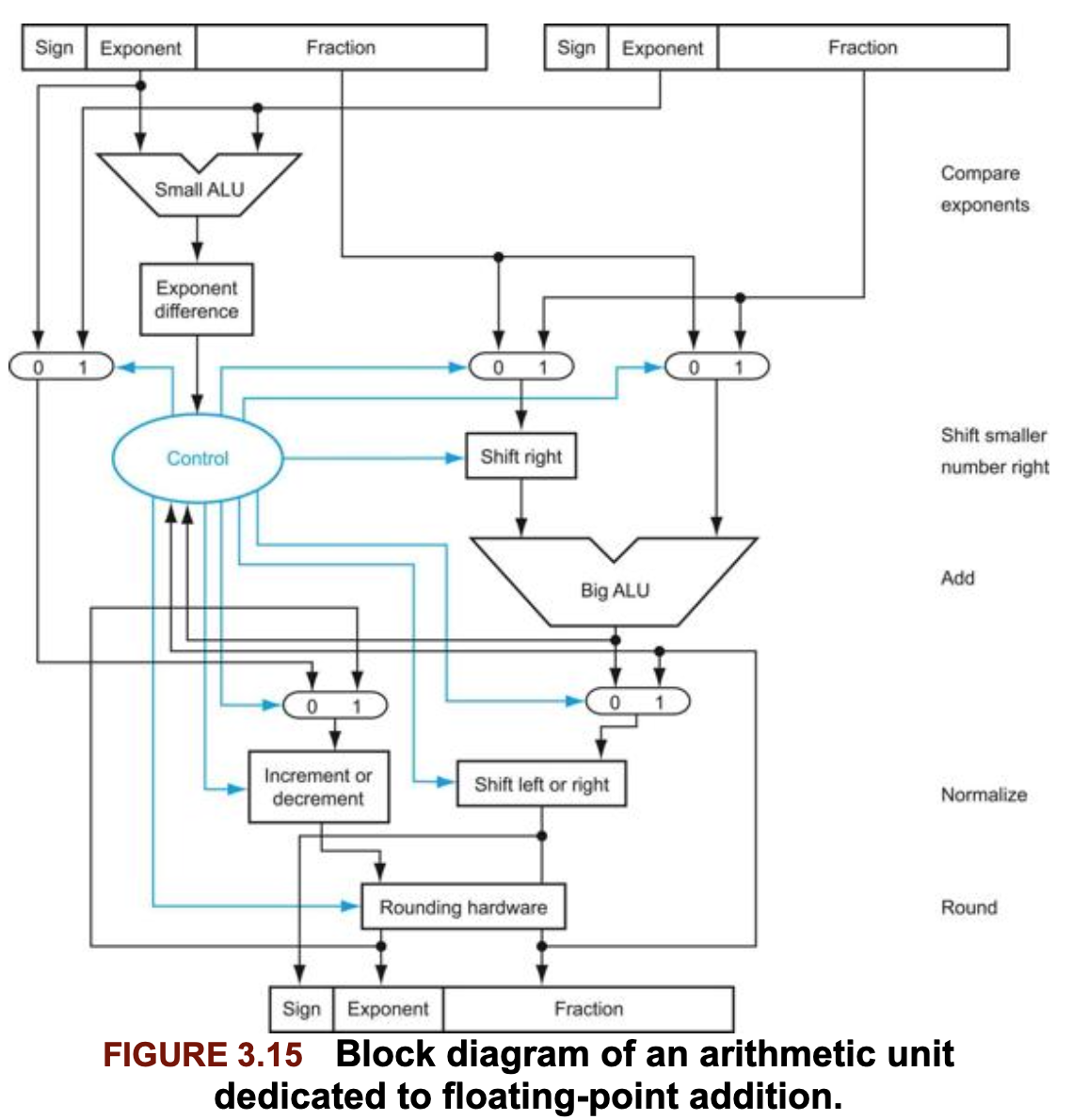
3.7 정확한 산술
가장 작은 수와 가장 큰 수 사이의 모든 수를 정확하게 나타낼 수 있는 정수와는 달리, 부동소수점 숫자는 실제로 나타낼 수 없는 수의 근사값인 것이 보통이다. 이는 0과 1 사이만 해도 무수히 많은 실수가 존재하기 때문이다.
따라서 실제의 수에 가장 근접한 부동 소수점 표현을 구해야 한다. 이를 위해서 IEEE754는 프로그래머가 원하는 근사 방법을 선택할 수 있도록 여러 가지 자리맞춤 방법을 제공한다.
정확한 계산을 위해서는 추가 비트를 포함하여야 한다.
IEEE754는 계산하는 동안 오른편에 항상 2개의 추가 비트를 유지한다. 이를 각각 guard bit와 round bit라 부른다.
이를 십진수 예시로 확인해보자.
3.7.1) 보호 자릿수를 사용한 자리맞춤
유효자리가 10진수 3자리라 가정하고, 2.34 x 10^2에 2.56 x 10^0을 더해보자. 유효자리 숫자 3자리를 사용하여 가장 가까운 십진수로 자리맞춤하라.
먼저 지수를 맞추기 위해서 작은수를 오른쪽으로 자리 이동 하여야 한다.
따라서 0.0256 x 10^2가 된다. guard bit와 round bit가 있기 때문에 지수를 정렬할 때 2개의 최하위 자리를 표현 수 있다.
guard bit는 5가 되고, round bit는 6이된다. 합은 다음과 같다.

따라서 결과는 2.3656 x 10^2가 돤다. 자리맞춤 할 두자리를 갖고 있기 때문에 0부터 49는 버리고 51부터 99는 올린다.
50은 tiebreaker 이므로 50%확률로 버리고, 50%의 확률로 올린다.
따라서 3자리 유효숫자로 자리맞춤한 결과는 2.37 x 10^2가 된다.
만약 guard bit와 round bit 이 없었다면, 두자리를 버리고 덧셈을 해야 한다.
2.34 + 0.02가 되어 2.36이 나왔을것이다.
자리맞춤 시 최악의 경우는 실제 값이 두 부동 소수점 표현의 중간이 되는 경우이다.
부동 소수점에서 정확도는 유효자리의 최하위 비트 중 오류가 발생한 것이 몇비트인가에 따라 결정된다.
이 척도를 ulp(units in the last place)라고 부른다.
3.7.2) 고난도
IEEE 754에는 "가장 가까운 짝수로의 자리맞춤(round to nearest even)"이 있다.
결과값이 정확히 두 값의 가운데에 위치하는 경우 어떻게 할 것인가를 결정한다. 미 국세청의 경우 항상 0.5달러를 자리올림한다. 따라서 국세청에게 이익이 돌아간다.
IEEE754 표준은 계산된 결과값이 두 값의 가운데에 위치할 때, 최 하위 비트가 홀수이면 더하기 1을 하고, 짝수이면 잘라내도록 한다.
정 가운데일때 이 방법은 항상 최 하위 비트를 0으로 만들어 준다. 이 방식이 가장 가까운 짝수로의 자리 맞춤 방식이다. Java는 이 방식만 지원한다.
마지막으로 guard bit와 round bit 외에 3번째 비트가 등장하는데, 바로 sticky bit 이다.
sticky bit는 자리 맞춤시 0.50...00 과 0.50...01을 구별할 수 있게 해준다.
3.7.3) 비정규화 수
0과 가장작은 정규화 수 사이에 존재하는 수를 표현하기 위해서 IEEE는 비정규화 수(denormalized number)를 허용한다.
이들 모두 지수가 0이지만, 유효자리는 0이 아니다. 이 방식은 숫자가 작아지면서 유효자리가 점점 줄어들어서 궁극적으로 0이 되는 것을 허용하는데 이를 점진적 언더플로우(gradual underflow)라 한다.
예를 들어 정규화된 양수 단일 정밀도 수 중에서 가장 작은 것은 다음과 같다.
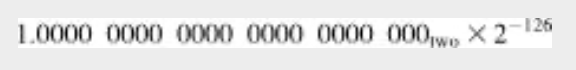
그러나 가장 작은 비정규화 수는 다음과 같다.
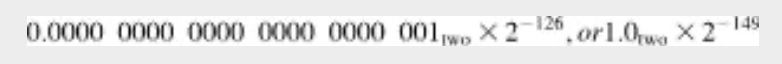
'CS > Computer Organization Design (2023-1)' 카테고리의 다른 글
| [컴퓨터 구조] 4. 프로세서 (0) | 2023.06.16 |
|---|---|
| [컴퓨터 구조] 2. 명령어: 컴퓨터 언어 (0) | 2023.04.17 |
| [컴퓨터 구조] 1. 컴퓨터 추상화 및 관련 기술 (1) | 2023.03.21 |

댓글