직접 풀어보고 올리는 코드입니다. 지적이나 더 좋은 방향에 대한 댓글은 항상 환영합니다.
14601번: 샤워실 바닥 깔기 (Large)
첫 번째 줄에는 바닥의 한 변의 길이를 표현하는 자연수 K(1 ≤ K ≤ 7) 가 주어진다. 이때 바닥의 크기는 2K 가 됨에 유의하라. 두 번째 줄에는 배수구의 위치를 나타내는 자연수 x, y (1 ≤ x, y ≤ 2K)
www.acmicpc.net
생각의 흐름
이번 문제는 문제를 해결하기에 앞서, 출력하는 부분부터 매우 거슬리는 문제이다.
보통 시작점을 왼쪽 상단으로 두는데, 이번 문제는 시작지점이 왼쪽 하단이다. 이점 또한 주의해야 한다.
우선 이번 문제를 해결하기 위해 L-트로미노에 대한 귀납적 증명글을 작성해 두었다 먼저 읽어보길 권장한다.
[알고리즘] L-트로미노
1. 트로미노란? " data-ke-type="html"> <>HTML 삽입 미리보기할 수 없는 소스 트로미노는 크기가 같은 정사각형 3개를 변끼리 붙여 만든 다각형 이다. 따라서 다음과 같은 모양이 가능하다. 2. 트로미노로
blogshine.tistory.com
위의 글에서 설명했듯, 주어진 정사각형에 L-트로미노를 채우는 방법은 한 변의 크기 N를 절반으로 줄인 N/2 짜리 부분 정사각형을 4개를 통해서 구할수가 있다.
다시 이 N/2 짜리 부분 정사각형을 해결하려면 N/4 짜리 4개가 필요하다.
따라서 하나의 문제를 해결하시 위해 지속적으로 더 작은 문제로 나눠야 하니, 분할정복에 해당되게 된다.
알고리즘은 다음과 같다.
1) 한변이 N짜리 정사각형을 한변이 N/2 짜리 4개의 부분 정사각형으로 나눈다.
2) 부분 정사각형 마다 -1(배관)이 있는지 확인한다.
-> 배관이 없다면 한변이 N짜리 정사각형의 중심부에 가장 가까운 위치를 숫자로 매꿔준다. 다음 그림을 보자.
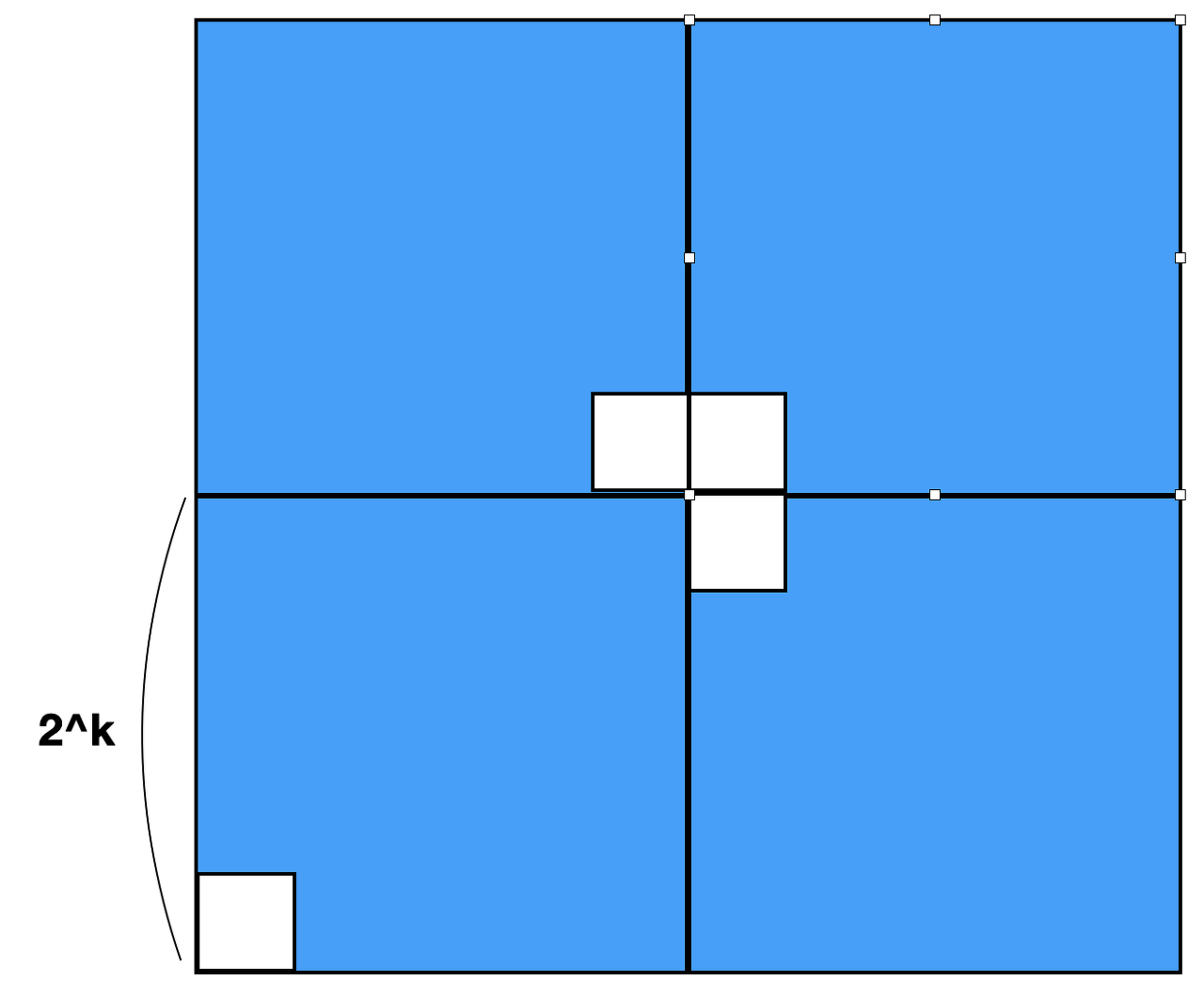
위 그림에서 왼쪽 하단의 정사각형 말고는 배관이 없다. 이부분들이 모여 하나의 L-트로미노를 중심에 만든다.
따라서 부분 정사각형의 위치를 기준으로 중심부분에 해당되는 곳에 숫자를 매꿔주어야 한다.
if (isNotDrain(x, y, halfLen)) MAP[x + halfLen - 1][y + halfLen - 1] = cnt;
if (isNotDrain(x, y + halfLen, halfLen)) MAP[x + halfLen - 1][y + halfLen] = cnt;
if (isNotDrain(x + halfLen, y, halfLen)) MAP[x + halfLen][y + halfLen - 1] = cnt;
if (isNotDrain(x + halfLen, y + halfLen, halfLen)) MAP[x + halfLen][y + halfLen] = cnt;-> 만약 배관이 있다면, 넘어간다.
3) 기존의 부분 정사각형을 기준으로 다시 각 부분정사각형을 4조각씩 나눈다. 이후 반복된다.
나의 코드
#include <bits/stdc++.h>
using namespace std;
#define MAX 257
int K, x, y;
int cnt;
int MAP[MAX][MAX];
bool isNotDrain(int x, int y, int len){
for(int i = x; i < x+len; i++){
for(int j = y; j < y+len; j++){
if(MAP[i][j] != 0){
return false;
}
}
}
return true;
}
void go(int x, int y, int len) {
++cnt;
int halfLen = len / 2;
if (isNotDrain(x, y, halfLen)) MAP[x + halfLen - 1][y + halfLen - 1] = cnt;
if (isNotDrain(x, y + halfLen, halfLen)) MAP[x + halfLen - 1][y + halfLen] = cnt;
if (isNotDrain(x + halfLen, y, halfLen)) MAP[x + halfLen][y + halfLen - 1] = cnt;
if (isNotDrain(x + halfLen, y + halfLen, halfLen)) MAP[x + halfLen][y + halfLen] = cnt;
// 재귀적으로 이 과정을 반복한다.
if (len == 2)return;
go(x, y, halfLen);
go(x + halfLen, y, halfLen);
go(x, y + halfLen, halfLen);
go(x + halfLen, y + halfLen, halfLen);
}
int main(){
ios_base::sync_with_stdio(0);
cin.tie(0);
cin >> K >> x >> y;
MAP[y-1][x-1] = -1;
go(0, 0, (1<<K));
for (int i = (1 << K)-1; i >= 0; i--) {
for (int j = 0; j < (1 << K); j++) {
cout << MAP[i][j] << " ";
}
cout << "\n";
}
return 0;
}'Algorithm > 백준' 카테고리의 다른 글
| [백준][C++] 1629번: 곱셈 <187> (0) | 2022.02.17 |
|---|---|
| [백준][C++] 16719번: ZOAC <186> (0) | 2022.02.14 |
| [백준][C++] 2261번: 가장 가까운 두 점 <184> (2) | 2022.02.12 |
| [백준][C++] 1939번: 중량제한 <183> (0) | 2022.02.07 |
| [백준][C++] 2661번: 좋은수열 <182> (0) | 2022.02.04 |

댓글