직접 풀어보고 올리는 코드입니다. 지적이나 더 좋은 방향에 대한 댓글은 항상 환영합니다.

2261번: 가장 가까운 두 점
첫째 줄에 자연수 n(2 ≤ n ≤ 100,000)이 주어진다. 다음 n개의 줄에는 차례로 각 점의 x, y좌표가 주어진다. 각각의 좌표는 절댓값이 10,000을 넘지 않는 정수이다. 여러 점이 같은 좌표를 가질 수도
www.acmicpc.net
아 이번문제 너무어렵다......
생각의 흐름
이번문제는 2가지 방식으로 구현이 가능한데, 라인 스위핑 알고리즘 or 분할정복으로 해결이 가능했다.
분할정복에 대한 개념은 있는 상황이라, 좀더 처음 접하는 개념인 라인 스위핑 알고리즘으로 접근하였다.
다음 글은 내가 정리해둔 라인스위핑에 대한 설명이다. 먼저 읽어보시면 도움이 될수도!
우선 좌표를 저장하기위한 용도로 set을 사용할 것 이다.
Set 은 중복되는 원소를 허용하지 않으면서 정렬하며 내부적으로 RedBlack-Tree로 구현된 자료구조다.
따라서 O(nlogn)에 삽입과 탐색이 가능하다.
우리의 문제에서는 여러 점이 같은 좌표를 갖을 수 있다고 했으며, 이 문제를 풀 때 활용했던 것이 x좌표 정렬과 y좌표 정렬이었다. 만약 하나의 좌표에 중복되는 점이 여러개 있을 경우 한 번만 탐색하면 되기 때문에 굳이 여러점을 갖고 있을 필요도 없을 뿐더러, 내부 원소를 정렬 된 상태로 유지시켜주기 때문에 활용하기에 안성맞춤인 자료구조다.
1) 정렬
x좌표 순으로 모든 점들을 정렬 한다.
이는 라인 스와핑이 정렬후 탐색 하는 방식에서 정렬을 진행해주는 것 이다.
x좌표로 정렬한 이유는 x값이 가장 작은 점부터 시작하여 그다음으로 x값이 작은 좌표 계속 를 확인 해 나가기 위함이다.
x좌표를 기준으로 vector가 정렬된 모습이 다음과 같다 생각해 보자.

2) 탐색
정렬된 대상을 기준으로 1회 탐색을 진행하면서 만나는 점마다 판단기준을 적용하여 가장 짧은 거리를 구해야 한다.
우선 vec[0]과 vec[1]사이의 거리가 1번 점까지 봤을때 가장 최소거리가 된다. 이를 minDist로 잡아둔다. 이 값을 6이라 해보자.
0, 1번 점은 확인한 지점이기 때문에 set에 저장해 둔다. set = {vec[0], vec[1]}
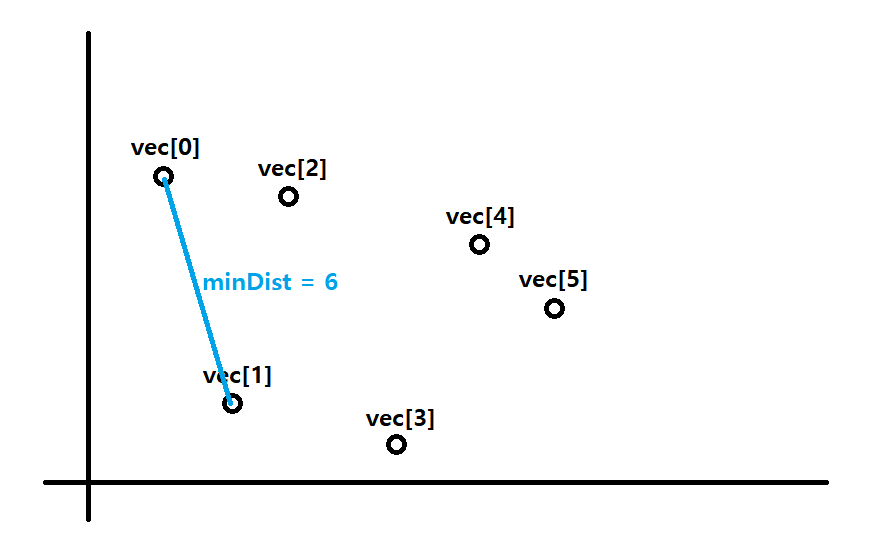
이제 다음 점인 vec[2]번 부터 판단기준을 적용하면서 vec[5]까지 확인해 보면 된다.
그럼 판단 기준은 무엇일까?
vec[2]를 기준으로 생각해보면
1) x좌표가 minDist 이내 거리에 있는 후보들을 선정한 뒤(밝은 회색 영역),
2) y좌표에 대해 (기준점의 y좌표 ± minDist) 거리 내에 있는 좌표을 뽑아(녹색 영역)
3) 기준점과 뽑힌 원소들과의 거리를 측정한 뒤 더 짧은 거리가 있다면 새 거리로 minDist를 갱신해주는 것이다.
이를 그림으로 보면 아래 그림과 같다.
(ps. 1번 과정에서 범위를 저렇게 잡는 이유는 가장 가까운 점의 거리가 minDist이기 때문에, 기준점의 x좌표와 차이가 minDist이하인 점만 후보가 될 수 있습니다. 이 후보를 그림으로 나타내면 다음 그림의 회색 영역에 해당합니다. 같습니다.)
(ps. 2번 과정에서 y의 범위는 왜 y+minDist, y-minDist에 해당될까? 이 또한 가장 가까운 점의 거리가 minDist 이기 때문에 y좌표와의 차이가 minDist이하인 점만 후보가 될 수 있기 때문이다. 이 후보의 영역까지 더해진 녹색영역이 우리가 탐색할 영역이다.)

이 과정에서 기존의 minDist보다 짧은 거리의 minDist를 발견하였기에 값 4로 갱신해 준다.
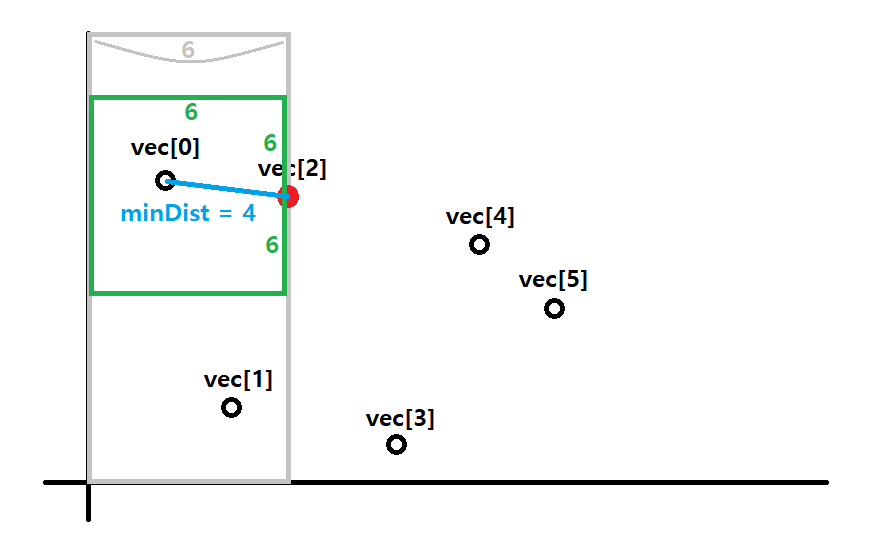
4) 판단 기준 적용이 끝나면 기준점 이였던 vec[2]는 set에 저장된다.
다시 vec[3]을 기준으로 잡은후 판단 기준을 다시 적용해 본다.

이번에는 범위 안에 있는 점이 없다. 따라서 minDist를 갱신해줄 필요가 없다.
다음 점인 vec[4]에서도 마찬가지로 범위안에 다른 점이 존재하지 않아 minDist를 갱신하지 않는다.
다시 vec[5]을 기준으로 잡은후 판단 기준을 다시 적용해 보자.
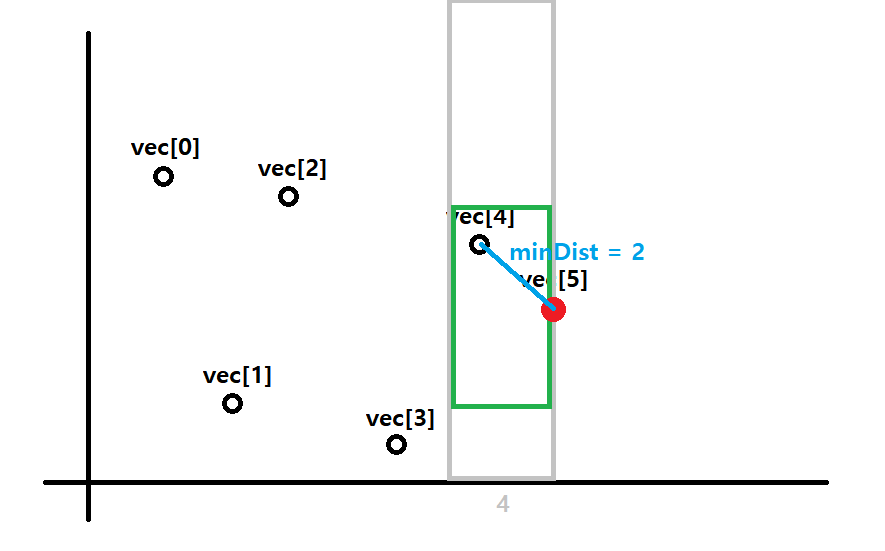
녹색 구간의 점인 vec[4]와 기준점인 vec[5]의 minDist가 2로 기존의 minDist였던 4보다 작은값이다.
따라서 minDist의 값을 2로 갱신해준다. 이러면 최소거리는 2로 찾게된 것 이다.
위에서 녹색 영역을 잡기 위해 y좌표에 minDist를 더하고 뺀후 lower_bound와 upper_bound 를 이용하여 녹색 영역에서
y값이 가장 작은 좌표와, y값이 가장 큰 좌표를 구해야 합니다.
int sqrtMinDist = (int)(sqrt((double)minDist) + 1);
auto up = s.upper_bound(Point(100000, nowP.y+sqrtMinDist));
auto low = s.lower_bound(Point(-100000, nowP.y-sqrtMinDist));lower_bound를 구할 때, x좌표에는 -100,000을 넣는 이유는 같은 y좌표를 가지는 점이 여러 개일 때, 가능한 x좌표의 값 중 가장 작은 값(-10,000)보다 작기 때문입니다. upper_bound도 마찬가지 입니다.
이렇게 구해진 up, low iterator를 이용하여 좌표들과의 거리를 구해본후 최소거리로 갱신해 줍니다.
while(low != up){
int tmpDist = dist(nowP, *low);
if(tmpDist < minDist){
minDist = tmpDist;
}
low++;
}
나의 코드
#include <bits/stdc++.h>
using namespace std;
class Point {
public:
int x, y;
public:
Point(int _x, int _y) : x(_x), y(_y) {
}
bool operator < (const Point& v) const {
if (y == v.y) {
return x < v.x;
} else {
return y < v.y;
}
}
};
int dist(Point p1, Point p2) {
return (p1.x-p2.x)*(p1.x-p2.x) + (p1.y-p2.y)*(p1.y-p2.y);
}
bool cmp(const Point& u, const Point& v) {
return u.x < v.x;
}
int main(){
ios_base::sync_with_stdio(0);
cin.tie(0);
int N;
cin >> N;
vector<Point> vec;
int a, b;
for(int i = 0; i < N; i++){
cin >> a >> b;
vec.push_back(Point(a, b));
}
sort(vec.begin(), vec.end(), cmp);
int minDist = dist(vec[0], vec[1]);
set<Point> s;
s.insert(vec[0]);
s.insert(vec[1]);
int start = 0;
for(int i = 2; i < N; i++){
Point nowP = vec[i];
while(start < i){
Point p = vec[start];
int gap = nowP.x - p.x;
if(gap*gap > minDist){
s.erase(p);
start++;
}else{
break;
}
}
int sqrtMinDist = (int)(sqrt((double)minDist) + 1);
auto up = s.upper_bound(Point(100000, nowP.y+sqrtMinDist));
auto low = s.lower_bound(Point(-100000, nowP.y-sqrtMinDist));
while(low != up){
int tmpDist = dist(nowP, *low);
if(tmpDist < minDist){
minDist = tmpDist;
}
low++;
}
s.insert(nowP);
}
cout << minDist << "\n";
return 0;
}'Algorithm > 백준' 카테고리의 다른 글
| [백준][C++] 16719번: ZOAC <186> (0) | 2022.02.14 |
|---|---|
| [백준][C++] 14601번: 샤워실 바닥 깔기 (Large) <185> (0) | 2022.02.13 |
| [백준][C++] 1939번: 중량제한 <183> (0) | 2022.02.07 |
| [백준][C++] 2661번: 좋은수열 <182> (0) | 2022.02.04 |
| [백준][C++] 3980번: 선발 명단 <181> (0) | 2022.02.03 |

댓글