
Two Pointers Algorithm
투 포인터 알고리즘은 기본적으로 1차원 배열상에서 배열을 가리키는 포인터 2개를 이용하는 방법 입니다!
(포인터 라고 해서 C의 그 포인터를 사용한다는 것 이 아닌, 배열의 어느 한칸을 가리키는 용도로 사용하는 것을 의미합니다)
2003번: 수들의 합 2
첫째 줄에 N(1 ≤ N ≤ 10,000), M(1 ≤ M ≤ 300,000,000)이 주어진다. 다음 줄에는 A[1], A[2], …, A[N]이 공백으로 분리되어 주어진다. 각각의 A[x]는 30,000을 넘지 않는 자연수이다.
www.acmicpc.net
대표적인 문제로 백준의 2003번이 있습니다. 이 설명을 보기전 문제를 먼저 한번 읽어주시면 감사하겠습니다!
다음과 같은 input이 있다고 가정해 봅시다.
10 5
1 2 3 4 2 5 3 1 1 2총 10개의 숫자가 있으며, 연속된 수의 합이 5가되는 경우의 수를 구해야 합니다.
우선 포인터 2개를 선정해 봅시다!
left, right 라는 포인터 2개를 사용할 예정입니다.
맨처음 두 포인터가 가리키는 배열의 index는 둘다 -1이며, sum값은 0으로 초기화 되어있습니다. 또한 항상 left <= right 이여야 합니다!
int left(-1), right(-1);
int sum = 0;포인터의 표기를 다음과 같이 할 생각입니다.
[a, b) : 이 표기의 뜻은 a초과(a는 포함안함) b이하(b포함) 을 의미합니다. 다만 a = b일 경우 크기가 0인, 아무것도 포함하지 않은 부분배열을 의미하게 됩니다. 시작지점을 포함하지 않고, 끝나는 부분은 포함하겠다 이 뜻 입니다!
알고리즘을 진행하면서 해야될 동작은 크게 3가지 입니다!
1) sum < 5
만약 현재 부분합이 5(M) 보다 작다면 right 포인터를 전진시킨 후 해당 arr[right] 값을 더해줍니다.
2) sum > 5
만약 현재 부분합이 5(M) 보다 크다면 left 포인터를 증가시킨 후 해당 arr[left]값을 빼줍니다.
3) sum = 5
만약 부분합이 5와 같다면 right 포인터를 증가시킨 후 해당 arr[right] 값을 더해줍니다.
(일부 다른 분들의 풀이를 보면 5와 값이 같은경우 left를 증가시킨후 값을 빼주는대 이렇게 하면 추가로 left index가 right index를 넘어서는 경우를 고려해야 합니다.)
left, right 포인터를 증가시키면서 부분배열의 합이 정확한지를 지속적으로 확인하는 것 입니다.
다음 그림을 통하여 시뮬레이션 해봅시다!
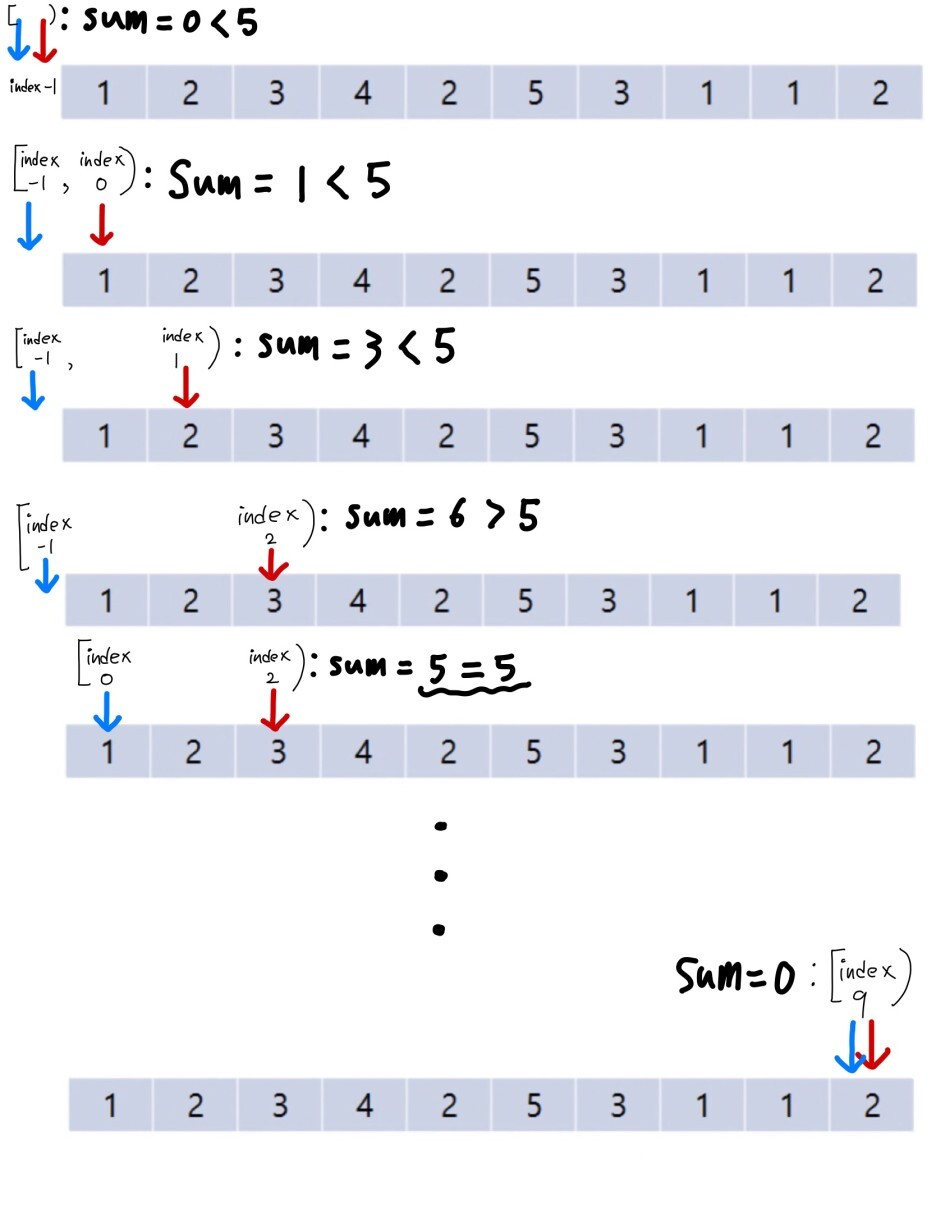
최종적으로 2개의 포인터 모두 index 9에 도달하게 되고, 종료되게 됩니다.
이 알고리즘의 시간복잡도는 얼마일까요? 바로! O(N) 입니다!
이 알고리즘은 매 loop마다 항상 두 포인터 중 하나는 1씩 증가하고 있고, 최악의 경우일지라도 각각 포인터가 N번씩 증가해서 배열의 끝에 도달해야만 알고리즘이 끝납니다.
따라서 각각 배열 끝에 다다르는 데 O(N)이라서 합쳐도 O(2N), 즉 O(N)안에 해결이 가능해 집니다!
코드로 확인해 봅시다!
#include <bits/stdc++.h>
using namespace std;
int arr[10001];
int N, M;
int cnt(0);
int main(){
ios_base::sync_with_stdio(0);
cin.tie(0);
cin >> N >> M;
for(int i = 0; i < N; i++)
cin >> arr[i];
int left(-1), right(-1);
int sum = 0;
while(left <= right && right < N){
if(sum > M) {
sum -= arr[++left];
}else if(sum < M){
sum += arr[++right];
}else if(sum == M){
cnt++;
sum += arr[++right];
}
}
cout << cnt;
return 0;
}'Algorithm > PS 알고리즘 정리' 카테고리의 다른 글
| [알고리즘] 비트마스크 조합, 부분수열 (0) | 2022.01.21 |
|---|---|
| [알고리즘] next_permutation : 다음 순열 (0) | 2022.01.21 |
| [알고리즘] Sweeping Algorithm : 라인 스위핑 알고리즘 (0) | 2022.01.21 |
| [알고리즘] Counting inversions (0) | 2022.01.21 |
| [알고리즘] lower_bound, upper_bound : C++ (0) | 2022.01.21 |

댓글