
Counting inversions
예를들어 배열A에 1, 2, 3, ... n 의 수가 무작위 순서로 들어있다고 해보자.
이 수들에서 2개의 무작위 수를 생각했을 때, 그 순서 대비 크기가 역전되어 있는 두 수의 쌍이 몇개가 되는지를 구해보자.
예를 들어 A {2, 3, 6, 4, 1, 7}이 있을때, 크기가 역전된 쌍은 (2, 1), (3, 1), (6, 4), (6, 1), (4, 1) 이 있다.
따라서 Inversion 된 쌍의 수는 5개 이다.
이런 Inversion된 쌍의 수를 어떻게 구해야 할까?
직관적으로 떠오르는 직접다 for문 돌면서 확인하는 방식은 O(n^2)이 걸릴것이 눈에 훤하다...
이럴때 Merge Sort를 활용하면 O(nlogn)에 가능해진다.
Merge Sort
Merge Sort를 진행하는 과정에서 교차점의 개수는 Inversion된 쌍의 수와 같습니다.
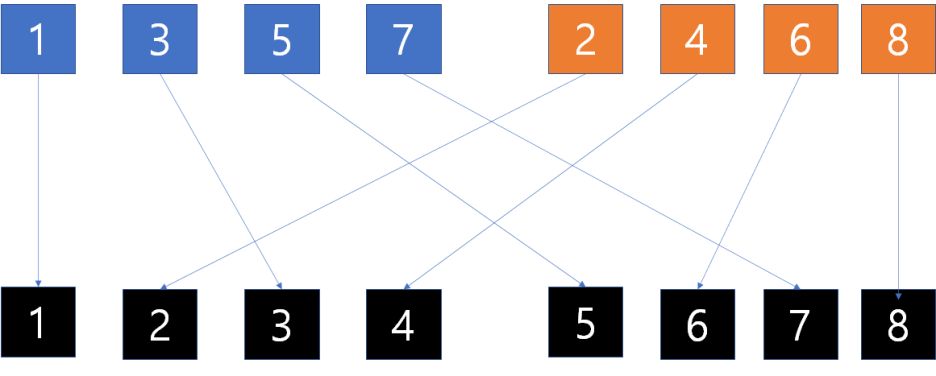
Merge Sort를 진행해 나가면서 배열의 두 수가 교환했다는 의미는 두 수의 순서가 바뀌어 있었다는 의미이니, 이는 역전된 쌍이였다는 것 이다
이 역전된 쌍 (a, b) 는 swap할 경우 위의 그림에서 보이듯 sorting 전 후 를 두고 선으로 연결했을때 교차지점이 생기게 된다.
이 교차지점들의 수가 inversion된 쌍의 수와 같게되는 것 이다.
위의 그림을 보면 3, 2는 역전된 쌍이며, 이들이 자리를 바꾸어 2, 3 순서가 될때 교차지점이 생기게 된다.
여기서 주의할 점이있다. swap할때 3, 2가 2, 3으로 바뀌었다고 해서 교차지점이 1개만 발생하는 것 이 아니다!!
당장 위의 예시만 봐도 2는 5, 7과도 교차지점이 생기게 된다!
위의 그림을 보면 파란쪽(1, 3, 5, 7) 과 주황쪽(2, 4, 6, 8) 로 나뉘어 있다.
파란쪽도 파란색배열 안에서는 정렬되어 있으며, 주황쪽도 주황색배열 안에서는 정렬되어 있는 상황이다.
여기서 주황색인 2가 3과 swap이 되면 파란배열안에서 3보다 큰 모든 수들과 교차치점이 생기게 된다.
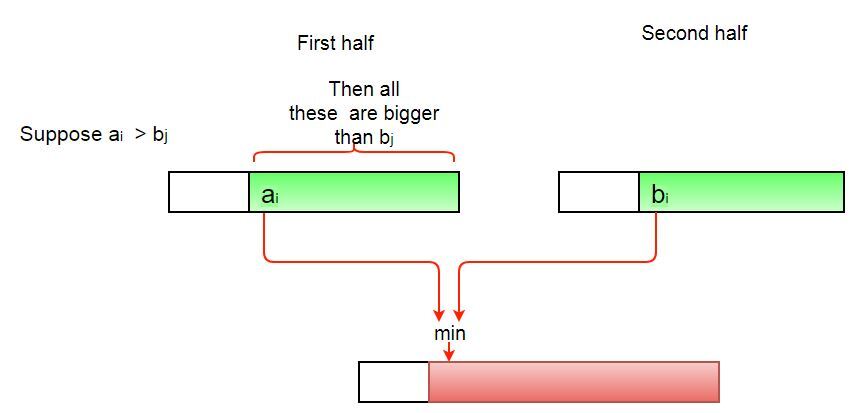
first half 배열에서 a 뒤의 값들은 모두 a보다 큰 상황이다.
여기서 a(3)보다 작은 b(2)를 a와 swap하면 당연히 a뒤의 값들(5, 7)과 교차지점이 발생하게 되는 것 이다.
백준의 다음 문제를 풀어보길 권장한다.
코드 구현
int arr[1000000];
int tmp[1000000];
long long merge(int left, int mid, int right){
int i = left, j = mid+1, k=left, l;
long long inversion_cnt = 0;
while(i <= mid && j <= right){
if (arr[i] <= arr[j]) {
tmp[k++] = arr[i++];
}else{
inversion_cnt += (long long)(mid - i + 1);
tmp[k++] = arr[j++];
}
}
if(i > mid){
for(l = j; l <= right; l++, k++){
tmp[k] = arr[l];
}
}else{
for(l = i; l <= mid; l++, k++){
tmp[k] = arr[l];
}
}
for (l = left; l <= right; l++)
arr[l] = tmp[l];
return inversion_cnt;
}
long long mergeSort(int left, int right){
long long inversion_cnt = 0;
if(left < right){
int mid = (left+right)/2;
inversion_cnt += mergeSort(left, mid);
inversion_cnt += mergeSort(mid+1, right);
inversion_cnt += merge(left, mid, right);
}
return inversion_cnt;
}'Algorithm > PS 알고리즘 정리' 카테고리의 다른 글
| [알고리즘] Two Pointers Algorithm : 투포인터 알고리즘 (0) | 2022.01.21 |
|---|---|
| [알고리즘] Sweeping Algorithm : 라인 스위핑 알고리즘 (0) | 2022.01.21 |
| [알고리즘] lower_bound, upper_bound : C++ (0) | 2022.01.21 |
| [알고리즘] 에라토스테네스의 체 : 소수 판별법 (0) | 2022.01.21 |
| [알고리즘] 트리의 지름 : Diameter of Tree (2) | 2022.01.20 |

댓글