[알고리즘] 비트마스크 조합, 부분수열

예전부터 비트마스크 활용하는거 정리 한번 해야지... 해야지 하다 안해서... 이번에 정리해본다.

먼저 부분수열부터 문제를 통하여 알아봅시다.

1. 비트마스크를 활용하여 부분 수열 구하기

 

1182번: 부분수열의 합

위 백준 문제를 통하여 설명해보겠습니다.

 

문제의 예시처럼 5개의 원소가 있다고 해봅시다.

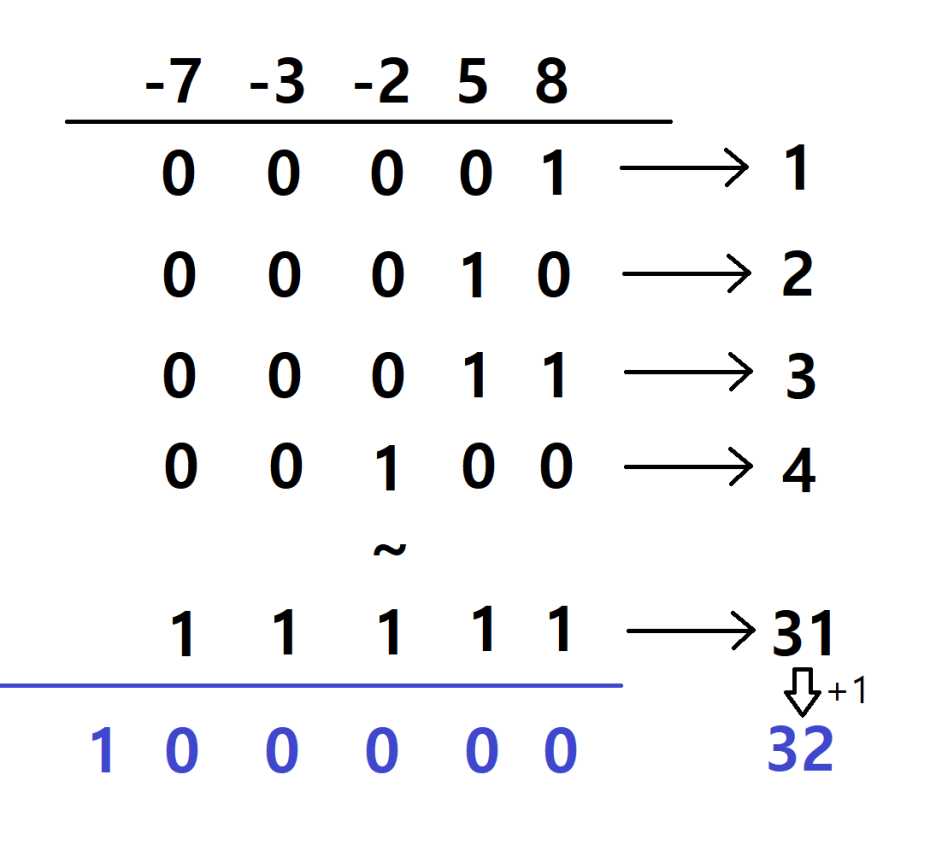
-7 -3 -2 5 8

 

각 원소 하나마다 (포함 or 미포함) 둘중 하나의 경우를 갖게되니, 총 2^N (N은 원소의 개수)개의 부분수열이 가능하다.

위 예시는 워소가 5개이니 32개의 부분수열이 가능하게 됩니다.

 

위의 5개의 원소가 포함된다면 1을 포함되지 않는다면 0으로 표현이 가능합니다. 다음과 같이 말이죠!

지금부터 상태와 표현값 이란 단어를 사용하겠습니다. (임의로 설명하기 위해 만든 단어 입니다)

상태는 2진수 표현이고, 표현값은 10진수 표현 입니다.

 

1) 8하나 고른

우리가 5개의 원소중,원소 8 하나만을 고른 상태(0, 0, 0, 0, 1)라고 해봅시다.

[8] 하나만 있겠죠? 이렇게 딱 8 하나만을 포함하고 있는 상태를 표현한 값, 즉 표현값이 1 입니다.

즉 우리는 표현값 1을 보고, 원소 8 하나만 포함된 상태임을 알 수 있죠!

 

2) 5와 8을 고른

우리가 5개의 원소중,원소 5, 8 두개를 고른 상태(0, 0, 0, 1, 1)라고 해봅시다.

[5, 8]이 있겠죠? 이렇게 2개의 원소를 포함하고 있는 상태를 표현한 값, 즉 표현값이 3 입니다.

즉 우리는 표현값 3을 보고, 원소 5, 8이 포함된 상태임을 알 수 있죠!

 

3) 모든 원소를 고른 상태

우리가 5개의 원소중, 원소 모두를 고른 상태(1, 1, 1, 1, 1)라고 해봅시다.

[-7, -3, -2, 5, 8]이 있겠죠? 이렇게 5개의 원소를 포함하고 있는 상태를 표현한 값, 즉 표현값이 31 입니다.

즉 우리는 표현값 31을 보고, 모든 원소가 포함된 상태임을 알 수 있죠!

 

이정도 봤으면 상태와 표현값이 뭘 의미하는지 감이 오셨겠죠?

 

이제 문제로 돌아가서, 우리는 모든 상태를 확인해봐야 합니다.

완전 탐색으로 모든 상태를 확인하면서 그 합을 하나하나 전부 구해서 비교하면 되는거죠!

따라서 코드의 구조는 다음과 같이 시작합니다.(문제에서 공집합은 제외 한다 하였으니 표현값0은 제외, 1부터 시작)

for (int i = 1; i < (1 << N); i++) // 문제에서 원소가 5개면 N은 5가 되겠죠?

 

위 코드는 표현값을 이용한것 입니다.

표현값 1 ~ 31 까지를 모두 확인 => 문제의 모든 상태를 확인한다는 의미가 됩니다.

 

 

이제 모든 표현값(=모든 상태)을 확인하면서 각각의 k번째 수가 포함되어있는지 판단해야 합니다.

 

예를들어 i = 1일때의 상태와 &연산을 진행하여 k번째 수가 포함되어있는지 판단할 수 있습니다.

이를 반복문을 통하여 다음과 같이 코드를 작성할 수 있습니다.

for(int i = 1; i < (1 << N); i++){
	int sum = 0;
	for(int k = 0; k < N; k++){ // i라는 표현값과 &연산을 하여 0 ~ N-1 까지 비교
		if(i & (1 << k)){
			sum += arr[k];
		}
	}
	if(sum == S) cnt++;
}

 

이제 전체 코드를 확인하면 다음과 같습니다.

#include <bits/stdc++.h>
using namespace std;

int N, S;
int arr[21];

int main(){
	ios_base::sync_with_stdio(0);
	cin.tie(0);
	
	cin >> N >> S;
	for(int i = 0; i < N; i++){
		cin >> arr[i];
	}
	int cnt = 0;
	
	for(int i = 1; i < (1 << N); i++){
		int sum = 0;
		for(int k = 0; k < N; k++){
			if(i & (1 << k)){
				sum += arr[k];
			}
		}
		if(sum == S) cnt++;
	}
	cout << cnt;
	return 0;
}

 

 

2. 비트마스크를 활용하여 조합 구하기

이것도 위 부분수열과 동일한 원리입니다. 이건 코드만 보여드리겠습니다.

int main(){
	ios_base::sync_with_stdio(0);
	cin.tie(0);
	freopen("input.txt", "rt", stdin);
	
	int N;
	cin >> N;
	int arr[4] = {1, 2, 3, 4};

	for(int i = 1; i < (1 << N); i++){
		for(int k = 0; k < N; k++){
			if(i & (1 << k)){
				cout << arr[k] << " ";
			}
		}
		cout << "\n";
	}

	return 0;
}

 

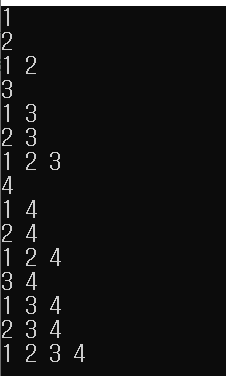
결과는 다음과 같다.

 

3. 비트마스크 연산 모음

현재 집합이 S일때

 

▶ i를 추가하는 경우

S | (1 << i)

 

▶ i를 검사하는 경우

S & (1 << i)

 

▶ i를 제거하는 경우

S & ~(1 << i)

 

▶ i를 토글 (0을 1로, 1을 0으로)

S ^ (1 << i)