[알고리즘] 트리의 지름 : Diameter of Tree

트리의 지름 이란?
트리의 지름은 두개의 말단노드간의 최장거리를 의미한다.
각각의 정점을 u, v 라고 한다면 이들간의 거리는 d(u, v) 라고 함수로 나타낼 수 있으며, 최장거리(지름)는 이러한 d(u, v) 값들중 최대인 Max d(u, v)라고 할 수 있다.
트리의 지름을 찾는 알고리즘
BFS(node) 를 통하여 node로 부터 가장 멀리있는 node를 구한다고 해보자.
이 방식은 greedy 방식에 해당된다.
< 알고리즘 >
1. 임의의 시작 정점 s로부터 가장 멀리있는 정점인 u를 BFS(s)로 구한다. (DFS도 가능)
2. 이렇게 구한 정점 u를 시작정점으로 하여 다시 BFS(u)를 구한다.
3. BFS(u)를 통하여 구해진 가장 멀리있는 정점 v를 얻었다면, 이렇게 구해진 정점 u와 v 사이의 거리가 최장거리이며 tree의 지름이다.
조금더 직관적으로 생각해 보자
다음 tree의 그림을 봐보자.
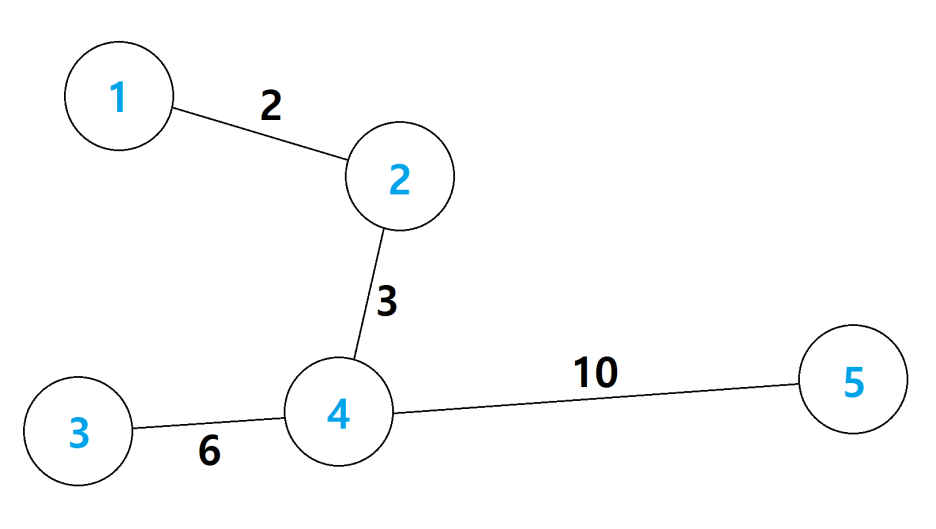
1) 우선 임의의 정점인 3번 정점으로부터 가장 멀리있는 정점은 5번 정점으로 그 거리는 16이다.
2) 정점 5에서 다시 최장거리인 곳을 찾으면 정점 3으로 그 거리는 16으로 가장 길다.
3) 트리의 지름은 16인 것 이다.
원을 생각해보면 한 원의 경계면인 끝에서 다른 끝 까지의 거리를 구한 느낌이라 느끼면 된다.
이번엔 다른 예시를 들어보자
1) 임의의 정점인 1번 정점으로부터 가장 멀리있는 정점은 5번으로 그 거리는 15이다.
2) 정점 5에서 다시 최장거리인 곳을 찾으면 정점 3으로 그 거리는 16으로 가장 길다.
3) 트리의 지름은 16인 것 이다.
이또한 원을 생각해보면, 원의 경계면 끝이 아닌, 원의 중심 어딘가에서 부터 최장거리를 구한 후, 그 끝에서부터 다시 끝까지의 거리를 구하는 느낌이다.
Proof by Contrdiction
트리의 특징을 2가지 정하고 가자
1. 트리에서 2개의 정점 사이의 경로는 오직 1개만 존재한다.
2. 모든 정점이 트리의 root 역할을 수행할 수 있다.
우리가 궁금한 것 은 위에서 언급한 알고리즘에서 왜 임의의 정점에서 BFS 탐색을 하면 가장 멀리 떨어진 정점에 도달하는가? 이다.
일단 루트에서 가장 거리가 먼 점 v가 만약 지름 안에 있다면, 그 점에서 가장 거리가 먼 점인 u까지의 경로가 지름이라는 것은 자명하다.
이제 이를 증명해 보자.
1. 왜 우리는 항상 BFS를 통하여 a로부터 반대편 끝인 b를 얻을 수 있는가?
--> 1. 두개의 노드 a, b를 사용하여 d(a, b)가 트리의 지름 이라고 해봅시다. 트리 속성으로 인해 a에서 b로 이동하는 고유한 경로가 오진 1개만 존재합니다.
--> 2. 우리가 임의의 정점 u에서 시작했다고 가정해 봅시다.
---> 1. 만약 u가 a라면, 우리는 알고리즘 BFS(a)를 통하여 항상 정점 b를 얻게되며, 2번째로 BFS를 실행하면 BFS(b)를 통하여 다시 a를 얻을수 있습니다.
이처럼 일단 루트에서 가장 거리가 먼 점 b가 만약 지름 안에 있다면, 그 점에서 가장 거리가 먼 점인 a까지의 경로가 지름이라는 것은 자명하다. 그래서 루트에서 가장 거리가 먼 점이 지름 안에 없다는 게(역) 모순이라는 것을 보이면 된다.
역을 생각해보자.
---> 2. 만약 u가 a가 아니고 and BFS탐색을 했을때 a, b와는 구별되는 다른 정점 v로 끝난다고 해봅시다.
위에서 a에서 b까지 가는 경로를 tree의 지름이라 불렀다. 그리고 지름에 있지 않은 정점 v는 정점 u로부터 가장 멀리 떨어진 정점이다.
또한 경로 (a, b)와 (u, v)는 중간에 t라는 정점에서 만난다고 가정해보자. 이러한 가정은 우리가 cycle을 만들지 않기위해서 a, b, u, v를 거치는 경로는 오직 t만을 공통으로 지난다고 가정하는 것 이다.
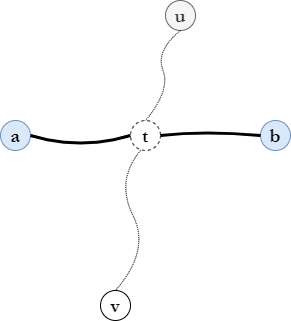
1) 두개의 노드 a, b를 사용하는 함수 d(a, b)가 트리의 직경임은 위에서 가정하였다, 정점 v는 d(u, v)를 통하여 u로부터 가장 멀다고 하였으니d(u, v)는 d(u, a)와 d(u, b)보다 큽니다.
2) 경로 (u, t)는 u로부터 출발하여 가는 모든 경로에서 공통으로 지나는 경로이며, 따라서 우리는 d(v, t) > d(a, t) 임을 알수있습니다.
(위에서 (u, v)가 가장 길다고 했으니까 정점t에서 가장 먼 곳은 v이다.)
3) 이것은 정점 v가 a에 비하여 b에서 부터 멀리 떨어저 있음을 의미하며, d(v, b) > d(a, b)가 됩니다.
(원래는 d(a, b)가 지름으로 가장 긴 상황인데, d(v, t) > d(a, t) 라고 하였으니 d(v, b) > d(a, b)가 됨)
4) 이것은 (a,b)가 지름 이란 우리의 초기 가정과 모순됩니다. 왜냐하면 우리가 더 긴 (v, b)를 찾았기 때문입니다.
대칭적으로 왜 d(v,a) > d(a,b)인지도 알 수 있습니다.
5) 따라서 만약 (a,b)가 실제 직경인 경우 정점 u로부터 가장 먼 정점은 a 또는 b가 되어야만 한다.
=> 위에서 역(루트에서 가장 거리가 먼 점이 지름 안에 없다) 을 언급했는데, 루트가 u였다고 생각하면 루트에서 가장 먼 지름을 만드는 정점 v가 지름에 없었으니 이는 모순이다.
역이 모순임을 밝혔으니, 원래의 가정이 참이 됩니다.
따라서 이 알고리즘은 지름을 구해줍니다.
(아 잠시만 내가 정확하게 생각한거인가?.............. 아 머리아프다.............. 이글은 태클 환영입니다!!)