[알고리즘] Red-Black Tree : 레드 블랙 트리
스스로 공부해 본 후, 다시 정리하는 내용의 글 입니다. 틀린부분과 실수가 있다면 지적해주시면 감사하겠습니다.

레드 블랙 트리 또한 binary-search tree(이진탐색트리) 의 일종이다.
기존의 이진탐색트리 같은경우 input이 이미 정렬되있다면 높이가 n이 되버리고, 따라서 시간복잡도 또한 O(n)에 도달하게 된다.

하지만 레드 블랙 트리의 경우 특정 조건을 지키면서 균형잡힌 이진트리가 되기때문에 Search, Insert, Delete 연산을 최악의 경우에도 O(logN) 시간안에 가능하도록 해준다.
이번 포스트의 순서는 다음과 같다.
1) NIL node 의 설명
2) Red-Black tree의 정의
3) Red-Black tree의 높이
4) Left and Right rotation
5) Insert 연산과 case 분류
6) Delete 연산과 case 분류
1. NIL node
우선 Red-Black tree를 설명하기 전에 NIL node에 대하여 정의하고 시작하자.
NIL node는 자식노드가 존재하지 않는경우 NIL node라는 특수한 노드가 있다고 생각하자.
따라서 모든 leaf node는 NIL node가 된다. 또한 root의 부모도 NIL node 라고 가정하자.
노드들은 내부노드와 NIL node로 나뉜다.
그림으로 보면 다음과 같을 것 이다.

2. Red-Black Tree의 정의
다음 5가지 조건을 만족하는 이진탐색트리를 Red-Black tree라고 부른다.
1) 각 노드의 색은 red 또는 black이다.
2) root 노드는 black이다.
3) 모든 말단노드(leaf node)는 black이다. (NIL이 black이 된다)
4) red 노드의 자식노드들은 전부 black이다. (즉, red 노드는 연속되어 등장할 수 없다.)
5) Root 노드에서 시작해서 자손인 leaf노드에 이르는 모든 경로에는 동일한 개수의 black노드가 존재한다.
마지막 5번의 의미가 잘 이해되지 않을 수 있다. 다음 그림을 통해 예를 들어보자.

위의 그림에서
case 1 : 13(b) → 8 → 11(b) → NIL(b) : 총 3개의 black노드를 거침
case 2 : 13(b) → 8 → 1(b) → 6 →NIL(b) : 총 3개의 black노드를 거침
case 3: 13(b) → 17 → 25(b) → 22 → NIL(b) : 총 3개의 black노드를 거침
root에서 NIL 까지 가는 경로상에서 만난 black노드의 수가 같은 것 이기 때문에 3으로 같다.
이들 case를 보면 경로를 통해 내려가는 동안 거친 black 노드의 수가 3개로 동일하다. 물론 몇가지 case가 더있지만 여기서는 생략하였다. 이들 또한 동일하다.
3. Red-Black Tree의 높이
높이를 2가지로 구분해볼수 있다.
1) h(x)는 x 자신으로부터 leaf 노드 까지의 가장 긴 경로에 포함된 edge(간선) 의 수 이다.
2) bh(x)는 x로부터 leaf 노드 까지의 경로상의 black노드의 개수 이다. (자기 자신 x는 빼고 count한다)
다음 그림을 통해 확인 해 보자.
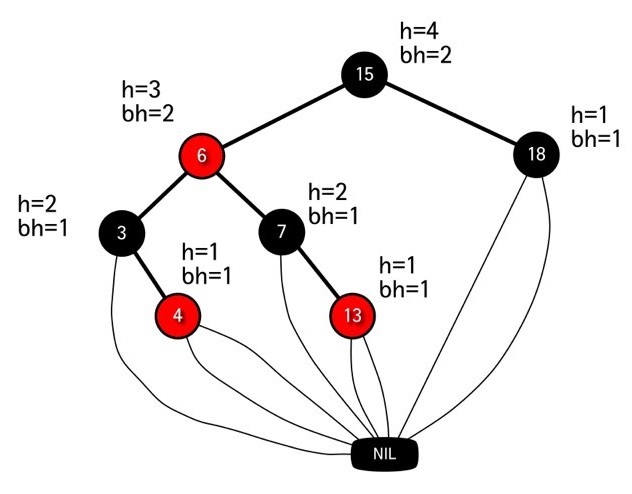
▶ 높이가 h인 노드의 bh는 bh >= h/2 이다.
조건 4에 의해 red노드는 2개가 연속해서 올수가 없다. red가 나오면 바로 black이 나와야 하니까 black 노드의 수가 적어도 절반 이상이 되야하는 것 이다.
▶ 노드 x를 root로 하는 임의의 subtree는 적어도 2^bh(x) -1 개의 내부 노드를 포함한다.
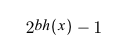
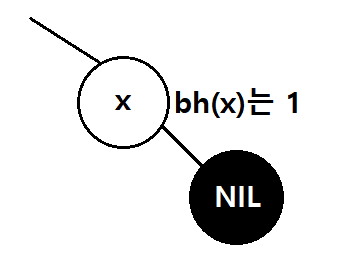
이는 x 자기 자신을 subtree의 내부 노드로 갖고있는 상황이다.
이를 수학적 귀납법 을 이용하면 tree 전체에 적용가능함을 알 수 있다.
▶ n개의 내부 노드를 갖는 red-black tree의 높이는 2log(n+1) 이하 이다.
한 트리의 총 노드의 수 n은 바로 위에서 배운 x를 루트로 하는 subtree의 노드의 수(2^bh-1)보다는 크거나 같다.
또한 bh는 바로 위에서 확인했듯 bh >= h/2 이다. 따라서 다음과 같은 식이 성립한다.
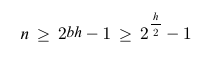
여기서 높이 h를 유도할 수 있다.

4. Left and Right Rotation
그림을 통해 한번에 확인 가능하다.

시간복잡도는 O(1)이며, 이진탐색트리의 특성을 그대로 유지한다.
Left-Rotate(T, x)
y <- right[x] // set y
right[x] <- left[y] // x의 오른쪽 자식을 y의 왼쪽 자식으로 지정
p[left[y]] <- x // β의 부모를 y에서 x로 변경
p[y] <- p[x] // x의 부모가 y의 부모노드가 됨
if p[x] = nil[T] // 만약 x의 부모가 NIL이라면, 즉 x가 root라면
then root[T] <- y // y가 새로운 tree의 root가 됨
else if x = left[p[x]] // x가 x의 부모의 왼쪽 자식이라면
then left[p[x]] <- y // y가 x부모의 왼쪽 자식이 되고
else right[p[x]] <- y // y가 x부모의 오른쪽 자식이 되고
left[y] <- x // x와 y를 연결
p[x] <- y
5. Insert
sudo 코드를 통해 우선 확인해보자. 미자막을 제외하고는 BST의 삽입과 동일하다.
RB-Insert(T, z) // z는 insert할 node
y <- nil[T]
x <- root[T]
while x ≠ nil[T] // x가 null이 아닌동안 계속
do y <- x
if key[z] < key[x]
then x <- left[x]
else x <- right[x]
p[z] <- y // 새로운 node를 y의 자식에 insert
if y = nil[T] // y가 null인 경우. 즉, 현재 tree가 비어있는 경우
then root[T] <- z // z가 root가 된다.
else if key[z] < key[y] // 원래 tree가 비어있지 않은경우
then left[y] <- z;
else right[y] <- z;
left[z] <- nil[T] // 삽입 후 leaf node가 되니, 양쪽 자식을 NIL로 설정
right[z] <- nil[T]
color[z] <- RED // 삽입된 z의 색은 red로
RB-Insert_Fixup(T, z)새로 삽입할 노드 z를 red로 칠해준다.
삽입이후에 우리의 tree는 RB tree의 조건 5가지를 만족해야 한다. 이를 확인해 보자.
1) 성립한다.
2) 만약 z가 root 노드라면 위반, 아니면 조건2는 성립한다.
새로 추가한 노드는 red 니까 보통의 경우에는 성립한다. 하지만, 원래 tree가 비어있는 경우 red가 root위치하게 된다. 이럴 때는 간단하게 그냥 root를 black으로 변경해주면 끝난다.
3) 성립한다.
4) 문제가 된다! 새로 삽입한 z의 부모y가 black이면 상관이 없는데, red이면 조건 위반이다. 다음 그림처럼 말이다.
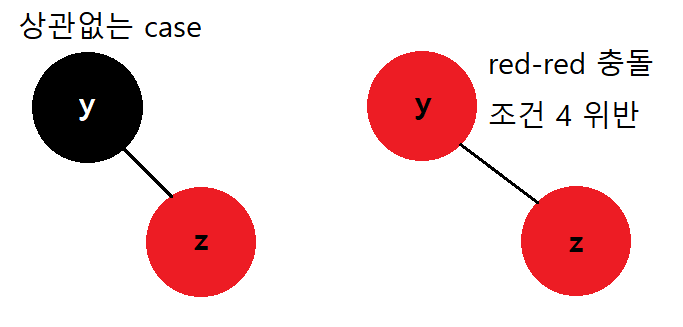
이런 red-red 충돌을 수정해주기 위해서 추가적인 RB-Insert_Fixup 이라는 함수를 호출해줘야 한다.
5) 성립한다.
▶ RB-Insert_Fixup 의 구현
우선 RB-Insert_Fixup 가 언제 종료되고, 언제 필요한지를 확인해보자.
- 필요한 경우
조건 2 위반, z가 root이면서 red인 경우.
조건 4 위반, z와 그 부모 p[z]가 둘다 red인 경우.
- 종료조건
부모노드 p[z]가 black이면 종료한다. 조건 2가 위반일 경우 z를 그냥 black 으로 변경해주면 끝난다.
총 3가지 case 가 insert에서 존제하게 된다.
참고로 case1,2,3 은 모두 p[z](아버지)가 p[p[z]](할아버지) 의 왼쪽 자식인 경우들 이다.
case 4,5,6은 p[z]가 p[p[z]]의 오른쪽 자식은 경우로, 그냥 좌우만 바꿔주면 된다. 따라서 case 1,2,3만 설명하겠다.
case 1 : z의 삼촌 y가 red인 경우
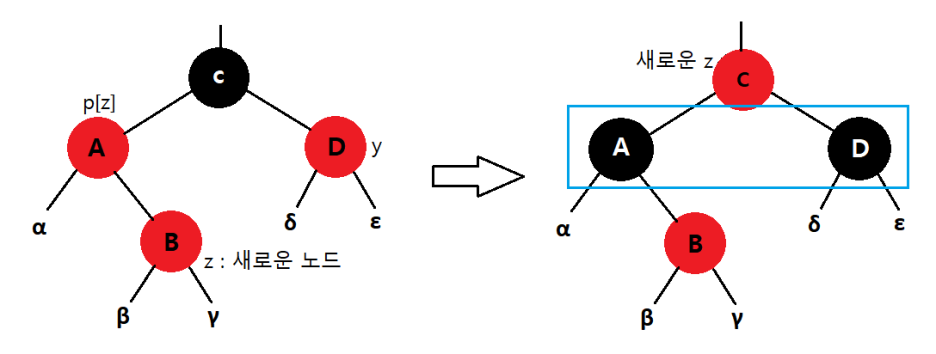
B노드가 우리가 새롭게 삽입한 z이다. 이 z는 A의 오른쪽 자식일수도 있고, 왼쪽 자식 일수도 있다.
위의 그림에서 A와 B가 red-red 충돌이 발생하고있고, z의 삼촌 y(D)가 red인 상황이다.
이는 A와 D를 black으로, 할아버지 C는 red로 변경해주면 A와 B 의 red-red충돌은 해결이 되었다.
하지만 완벽한 해결이 아니다. 왜냐하면 할아버지 노드인 C가 red가 되면 p[c]와 red-red 충돌이 발생할 수 있기 때문이다.
다만 이렇게 색을 변경해 주면, red-red 충돌의 문제가 위로 2칸 이동해 있음을 알수있다.
즉, A-B의 문제가 C-p[C] 간의 문제로 이동하였다. 이렇게 쭉 root까지 이동하게 되면 결국 마지막에는 root의 색만 그냥 black으로 변경해주면 끝나버린다.
또한 조건 5인 black height 또한 바뀌지 않는다. 색 변경 전이나, 변경후 모두 NIL 노드 까지 가는 경로의 black node의 수는 동일하다. C위에서 오던 중이라 생각하고 아래로 내려가면서 black의 수를 새보면 똑같다.
참고로 αβγδε 의 경우 부모가 red이니까 이들은 black이다. 연속된 red는 불가능 하니까 이는 당연하다.
case 2, 3 : z의 삼촌 y가 Black인 경우
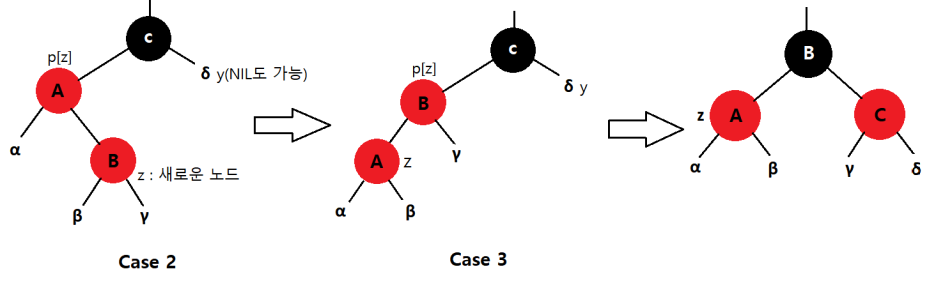
삼촌 y는 NIL node도 가능하기 때문에 검정 동그라미로 표현하지는 않았다. 어찌됬든 black이 라고 생각하면 된다.
- case2 : z가 오른쪽 자식인 경우
p[z]에 대하여 left-rotation한 후, 원래 p[z](A)를 z로 변경한다. 이후 case 3으로 진행한다.
- case3 : z가 왼쪽 자식인 경우
p[z](B)를 black, p[p[z]](C)를 red로 바꿈, 이후 p[p[z]](C)에 대하여 right-rotation을 진행. 최종 결과가 나온다.
지금까지의 설명한 RB-Insert_Fixup함수의 sudo코드를 확인해 보자.
RB-Insert-Fixup(T, z) // z는 새로 삽입하는 node
while color[p[z]] = RED
do if p[z] = left[p[p[z]]] // 할아버지의 왼쪽 자식이 Z의 부모인 동안, 즉 case 1,2,3
then y <- right[p[p[z]]] // 삼촌 y를 설정
if color[y] = RED // case 1의 경우
then color[p[z]] <- black // z의 부모를 black으로
color[y] <- black // 삼촌도 black으로
color[p[p[z]]] <- RED // 할아버지는 red로
z <- p[p[z]] // 할아버지를 새로운 Z로 설정
else if z = right[p[z]] // 내가 내 부모의 오른쪽 자식인 경우
then z <- p[z] // 내 부모를 z로 설정 // case2
Left-Rotate(T, z)
color[p[z]] <- Black // case3
color[p[p[z]]] <- RED
Right-Rotate(T, p[p[z]])
else (same as then clause with "right" and "left" exchanged)
color[root[T]] <- BLACK▶ Insert의 시간 복잡도
RB-Insert_Fixup
case1 의 경우 z가 2 level만큼 상승한다. case2,3 의 경우 상수시간이 걸린다. 따라서 트리의 높이에 비례하는 시간이 걸린다.
왜냐하면 최악의 겨우 case1이 계속 반복되어 root까지 red-red충돌을 올려야 할수도있다. 최종적으로 root까지 도달하면 root의 색만 black으로 변경해주면 된다. 따라서 최악의 경우는 높이에 해당할 것 이다.
시간복잡도는 O(logN)에 해당하게 된다.
마지막으로 insert의 예시를 확인해보자. 흰색 노드가 red이다.
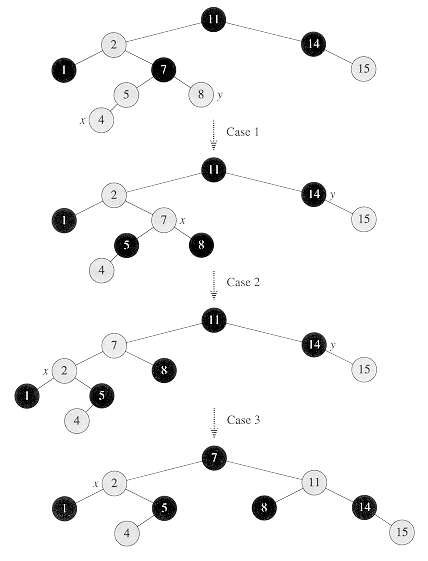
DELETE
sudo 코드를 통해 우선 확인해보자. 마자막을 제외하고는 BST(이진탐색트리)의 삽입과 동일하다.
참고로 다음 코드에서 나오는 successor 라는 함수는 삭제할 y의 바로 다음값,
즉 트리의 원소들을 오름차순으로 배열했을 때 y 바로 값을 의미한다.
예를 들어 tree의 모든 원소들을 오름차순으로 배열했을때 1, 2, 5, 7(y), 8, 11 순으로 있다면, y의 successor는 8에 해당한다.
RB-Delete(T, z) // z는 삭제할 노드의 주소. 이미 search는 완료된 상태
if left[z] = nil[T] or right[z] = nil[T] // 삭제할 노드 z의 자식이 하나 이하인 경우
then y <- z // y가 실제로 삭제할 node가 된다.
else y <- Tree-Successor(z)
if left[y] ≠ NIL // 왼쪽 자식이 존제한다면
then x <- left[y]
else x <- right[y]
if x ≠ NIL // 자식이 있는경우
then p[x] <- p[y] // y의 부모가 x의 부모가 됨
if p[y] = NIL // y가 root라면
then root[T] <- x // x가 root가 되어야 함
else if y = left[p[y]] // y가 자신의 부모의 왼쪽 자식이라면
then left[p[y]] <- x
else right[p[y]] <- x
if y ≠ Z // 원래 삭제하려는 z와 y가 다른경우
then key[z] <- key[y] // y의 successor의 data를 z로 옮김
copy y's satellite data into z
if color[y] = BLACK
then RB-Delete-Fixup(T, x)
return y실제로 삭제된 노드 y가 red였다면 그냥 종료하면된다. red는 연속할수가 없으니, red의 자식과 부모는 black일 것 이며 따라서 중간의 red를 지워도 black-black의 연속은 문제되지 않는다.
하지만! y가 black이였다면 RB-Delete-Fixup을 호출해줘야 한다. 이는 다음 그림을 보면 좀더 이해갈 것 이다.
(y는 삭제할 노드이고, x는 y의 자식이다.)
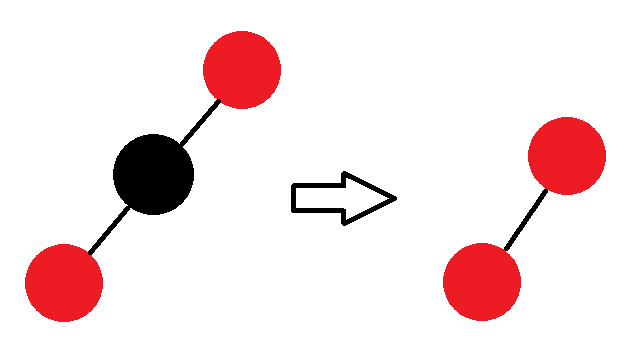
중간의 black노드를 삭제하면 red-red충돌이 발생하여 조건4를 위반하게 된다.
또한 조건(5) 의 문제도 추가적으로 생긴다. 갑자기 중간에 black 하나가 사라졌지 않는가?
이 두가지 문제를 해결해주기 위해 RB-Delete-Fixup을 호출해 준다.
삭제 이후에 우리의 tree는 RB tree의 조건 5가지를 만족해야 한다. 이를 확인해 보자.
1) 성립한다.
2) y가 root였고, x가 red인 경우 위반이다.
y가 삭제되고 나면 그자리를 x가 차지한다. 즉 x가 root 된 것 이다. 하지만 x의 색은 red이다. root는 red가 될 수 없다. 이는 간단하게 새롭게 root가 된 x의 색을 black으로 변경해주면 끝난다.
3) 성립한다.
4) p[y]와 x가 모두 red일 경우 성립하지 않는다. 이는 바로 직전에서 보인 그림의 경우에 해당한다.
5) 원래 y(black)를 포함했던 모든 경로는 이제 black노드가 하나 부족하다.
- 노드 x에 "extra black"을 부여해서 일단 조건 5를 억지로 라도 만족시킨다. 다음 그림을 통해 확인해 보자.
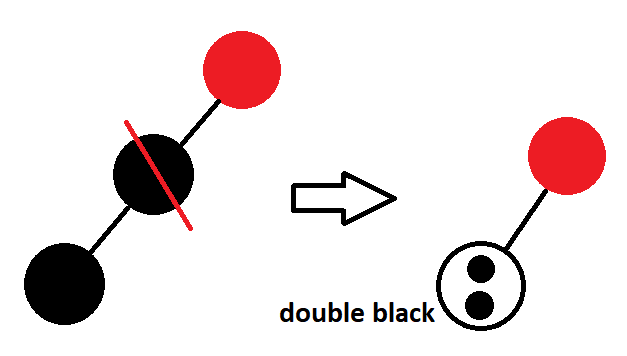
위의 그림을 보면 검정 노드가 하나 삭제되어 black height가 문제되는데, 이를 막고자 한노드에 2개의 black 노드를 삽입했다고 우선 생각하자.
▶ RB-Delete-Fixup 의 구현
아이디어
- extra black을 트리의 위쪽으로 올려보낸다. 올려보내다가 해당노드 x가 red&black이 되면 그냥 black노드로 만들고 끝낸다.
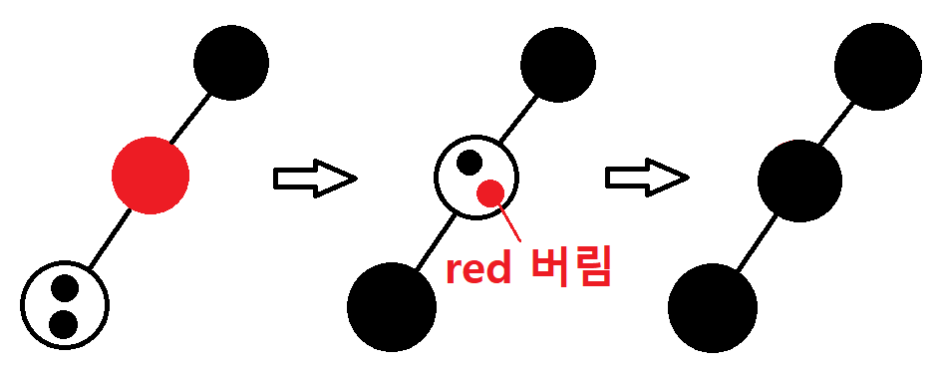
- 계속 올리다가 root에 도달하면 그냥 extra black을 제거한다.
이를 그림으로 확인해 보면 다음과 같다. 가장 상단이 root 라고 생각하자.
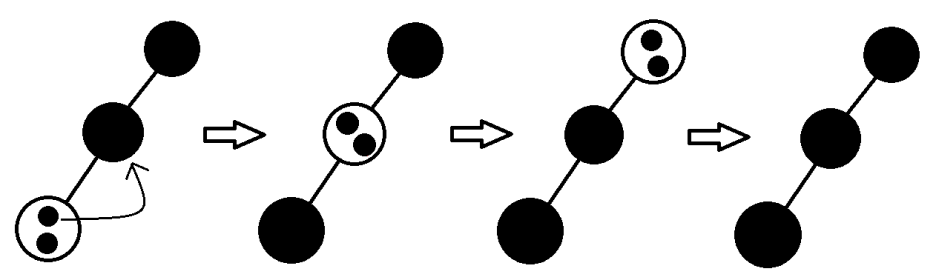
Loop Invariant (함수가 도는동안의 불변의 조건)
- x는 루트가 아닌 double-black 노드
- w는 x의 형제 노드
- w는 NIL노드가 될 수 없다. (만약 NIL이 되버리면 조건 5를 위반하게 된다.)
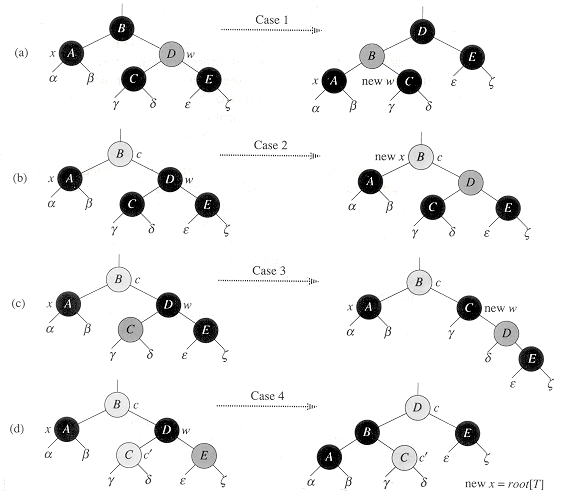
총 4가지 case 가 Delete에서 존제하게 된다.
참고로 case1,2,3,4 는 모두 x가 부모의 왼쪽 자식인 경우들 이다.
case 5,6,7,8은 x가 부모의 오른쪽 자식은 경우로, 그냥 좌우만 바꿔주면 된다. 따라서 case 1,2,3,4 만 설명하겠다.
case 1 : w가 red인 경우
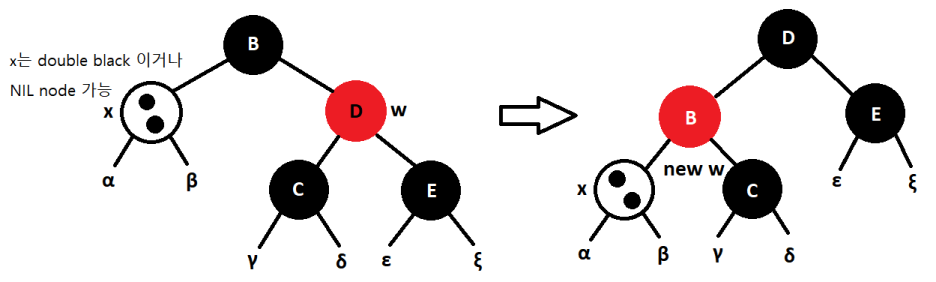
w의 자식들은 black이다. 이들은 NIL일수가 없다. NIL인 경우 조건 5에 위배된다.
이후 w(D)를 black으로 변경해 준후, p[x](B)를 red로 변경한다. 이후 p[x]를 기준으로 left-rotation을 적용한다.
기존의 w의 자식이였던 C는 B의 자식으로 편입되었다.
이후 case 2, 3, 4로 진행된다.
case 2 : w가 Black, w의 자식들도 Black
회색 노드는 Black일수도 있고, Red일수도 있다.
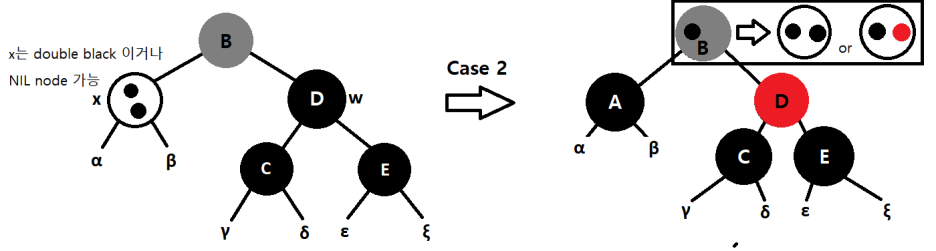
x의 extra-black을 p[x](B)에게 전달하고, w를 red로 바꾼다. p[x](B)를 새로운 x로 지정한다.
만약 case1에서 이 경우에 도착했다면 p[x]는 red였고, 따라서 새로운 x는 red&black이 되었다. 그냥 black으로 변경 후 끝.
case 3 : w는 Black, w의 왼쪽자식이 red
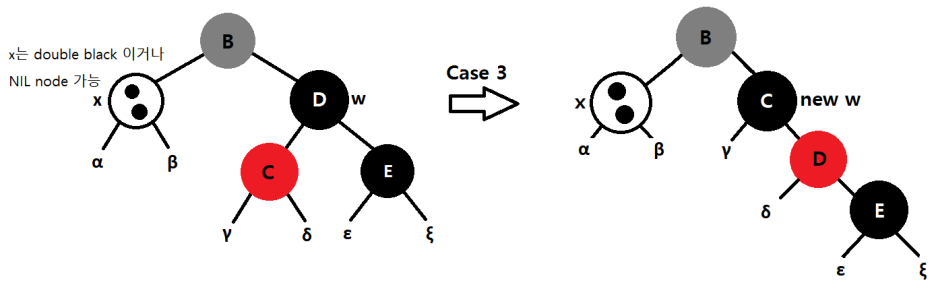
w를 red로 변경한고 w의 왼쪽 자식을 black으로 변경한다. 이후 w에 대하여 right-rotation 을 적용한다.
x의 새로운 형제 w는 오른쪽 자식이 red이다. 이는 case4에 해당하는 상황이다.
case 4 : w는 Black, w의 오른자식이 red
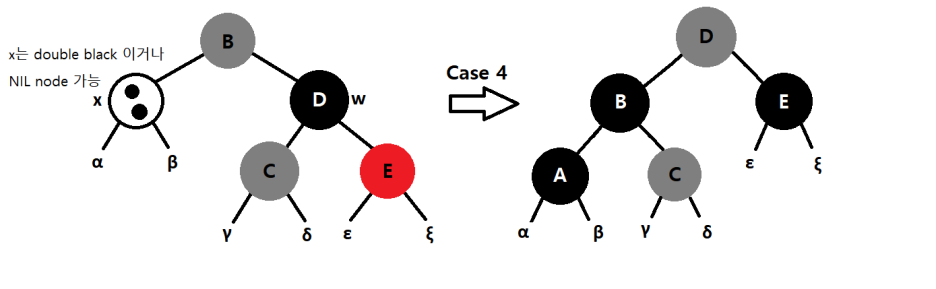
w와 B의 색을 교환(w의 색을 현재 p[x](B)의 색으로 변경, B의 색을 w의색인 black으로변경),
w의 오른쪽 자식(E)을 black으로 변경
p[x]에 대하여 left-rotation 적용후, x의 extra black을 제거한후 종료한다. (따라서 black height 유지 가능)
지금까지의 설명한 RB-Delete-Fixup함수의 sudo코드를 확인해 보자.
RB-Delete-Fixup(T, x) // x는 실제로 삭제한 y의 자식 노드
while x ≠ root[T] and color[x] = Black
do if x = left[p[x]] // 노드 x가 자신의 부모의 왼쪽 자식인 경우
then w <- right[p[x]] // 노드 x의 형제를 w라고 한다.
if color[w] = RED // 그 형제가 red인 경우 : case 1
then color[w] <- Black
color[p[x]] <- RED
Left-Rotate(T, p[x])
w <- right[p[x]] // 새로운 w 지정
if color[left[w]] = Black and color[right[w]] = Black // w의 두 자식이 black인 경우
then color[w] <- RED // w를 red로 변경
x <- p[x] // p[x]가 새로운 x가 됨.
else if color[right[w]] = Black // w의 오른쪽 자식이 Black인 경우
then color[left[w]] <- Black // 색 교환
color[w] <- Red
Right-Rotate(T, w)
w <- right[p[x]] // w가 p[x]의 새로운 오른쪽 자식이됨
color[w] <- color[p[x]]
color[p[x]] <- Black
color[right[w]] <- Black
Left-Rotate(T, p[x])
x <- root[T] // 그냥 while문 탈출 용도. 현재 tree의 root node를 새로운 x라고 한다.
else (same as then clause with "right" and "left" exchanged)
color[x] <- Black // x가 red이거나, double black인 경우 그냥 black으로 변경마지막으로 예시를 확인해보자. 회색 노드가 red, 진한회색은 red&black 또는 black&black 이다.
RB-Delete-Fixup 또한 O(logN)의 시간을 보장한다.