직접 풀어보고 올리는 코드입니다. 지적이나 더 좋은 방향에 대한 댓글은 항상 환영합니다.

https://www.acmicpc.net/problem/14002
14002번: 가장 긴 증가하는 부분 수열 4
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이
www.acmicpc.net
생각의 흐름
이번 문제의 핵심은 역추적을 어떤 방식으로 진행할것이지? 이다.
우선 점화식을 세워보면, DP[i]는 A[1] ... A[i]까지 수열이 있을 때, A[i]를 마지막으로 하는 가장 긴 증가하는 부분수열 길이 이다.
따라서 DP[i] = max(DP[i], DP[j] +1), 0< j < i, 를 통해서 DP[i]값을 구할 수 있다
이때 max연산을 통해서 값이 갱신이 될때를 잘 저장해둬야 한다.
어떠한 값이 왜 변경되었는지를 기록해야 역추적 하여 배열을 만들 수 있다.
res[i]는 A[i]의 앞에와야 하는 수의 index를 의미하게 된다.
우리 문제의 예시를 살펴보자.
6
10 20 10 30 20 50이를 그림으로 그려보면 다음과 같다.
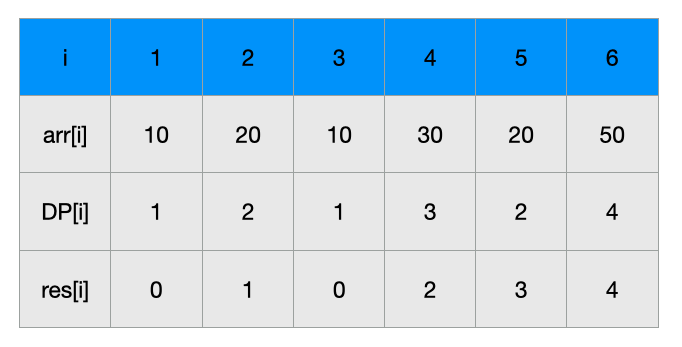
자기 앞에 오게 되는 수의 index i를 저장하는 것 이다.
나의 코드
1) C++
#include <bits/stdc++.h>
using namespace std;
int N;
int arr[1001];
int DP[1001];
int res[1001];
void show(int i) {
if(res[i] != 0) {
show(res[i]);
}
cout << arr[i] << " ";
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cin >> N;
for(int i = 1; i <= N; i++) {
cin >> arr[i];
}
DP[1] = 1;
for(int i = 2; i <= N; i++) {
DP[i] = 1;
int idx = 0;
for(int j = i-1; j > 0; j--) {
if(arr[i] > arr[j] && DP[j] + 1 > DP[i]) {
DP[i] = DP[j] + 1;
idx = j;
}
}
res[i] = idx;
}
int ans = 0;
int idx = 0;
for(int i = 1; i <= N; i++) {
if(DP[i] > ans) {
ans = DP[i];
idx = i;
}
}
cout << ans << "\n";
show(idx);
return 0;
}2) Python
import sys
N = int(sys.stdin.readline())
arr = [0] + list(map(int, sys.stdin.readline().split()))
DP = [0 for _ in range(N + 1)]
res = [0 for _ in range(N + 1)]
def show(idx):
if res[idx] != 0:
show(res[idx])
print(arr[idx], end=' ')
for i in range(1, N + 1):
idx = 0
DP[i] = 1
for j in range(i - 1, 0, -1):
if arr[i] > arr[j] and DP[i] < DP[j] + 1:
DP[i] = DP[j] + 1
idx = j
res[i] = idx
ans = max(DP)
p = [i for i, value in enumerate(DP) if value == ans][0]
print(ans)
show(p)'Algorithm > 백준' 카테고리의 다른 글
| [백준][C++/Python] 2225번: 합분해 (254) (0) | 2022.10.12 |
|---|---|
| [백준][C++/Python] 1912번: 연속합 (253) (0) | 2022.10.12 |
| [백준][C++/Python] 1655번: 가운데를 말해요 (251) (0) | 2022.10.10 |
| [백준][C++] 스타트와 링크 (246) (0) | 2022.09.22 |
| [백준][C++] 6593번: 상범 빌딩 <242> (0) | 2022.09.05 |

댓글