내돈내고 내가 공부한것을 올리며, 중요한 단원은 저 자신도 곱씹어 볼겸 가겹게 포스팅 하겠습니다.

10장. 힙(Heap)
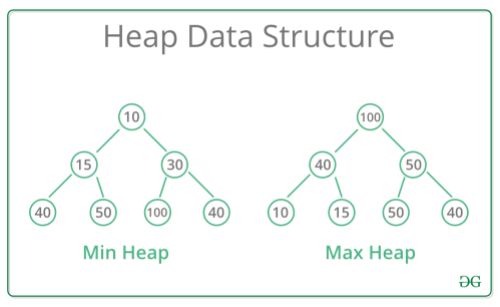
힙은 부모 노드의 키 값이 자식 노드의 키 값보다 큰(or작은) 이진트리 를 말한다. A가 B의 부모 노드라고 가정하면,
key(A) >= key(B) 인경우가 최대 힙이 되며, key(A) <= key(B) 인경우가 최소 힙이 된다.
Heap의 ADT
데이터: 우선순위를 가진 요소들의 모음
연산:
- insert(item): 우선순위 큐에 항목 item을 추가한다.
- remove(): 우선순위 큐로부터 가장 우선순위가 높은 요소를 삭제하고 이 요소를 반환한다.
- find(): 우선순위가 가장 높은 요소를 삭제하지 않고 반환만 한다.
- isEmpty(): 우선순위 큐가 공백 상태인지를 검사한다.
- isFull(): 우선순위 큐가 포화 상태인지를 검사한다.
- display(): 우선순위 큐의 모든 요소들을 출력.
최대 힙에서의 삽입 알고리즘
insert(key)
heapSize <- heapSize + 1;
i <- heapSize;
node[i] <- key;
while i ≠ 1 and node[i] > node[PARENT(i)] do
node[i] ↔ node[PARENT(i)];
i <- PARENT(i);힙 트리에서의 삭제 알고리즘
remove()
item <- A[1];
A[1] <- A[heapSize];
heapSize <- heapSize-1;
i <- 2;
while i <= heapSize do
if i < heapSize and A[LEFT(i)] > A[RIGHT(i)]
then largest <- LEFT(i);
else largest <- RIGHT(i);
if A[PARENT(largest)] > A[largest]
then break;
A[PARENT(largest)] ↔ A[largest];
i <- LEFT(largest);
return item;
HeapNode.h
#pragma once
#include <iostream>
#include <cstdio>
class HeapNode {
int key;
public:
HeapNode(int k=0) : key(k) {}
void setKey(int k) { key = k; }
int getkey() { return key; }
void display() { printf("%4d", key); }
};
MaxHeap.h
#pragma once
#include "HeapNode.h"
const int max_element = 200;
class MaxHeap {
HeapNode node[max_element];
int size;
public:
MaxHeap() : size(0) {}
bool isEmpty() { return size == 0; }
bool isFull() { return size == max_element; }
HeapNode& getParent(int i) { return node[i / 2]; }
HeapNode& getLeft(int i) { return node[i * 2]; }
HeapNode& getRight(int i) { return node[i * 2 + 1]; }
void insert(const int& key);
HeapNode remove();
HeapNode find() { return node[1]; }
void display();
};
void MaxHeap::insert(const int& key)
{
if (isFull()) return;
int i = ++size;
while (i != 1 && key > getParent(i).getkey()) {
node[i] = getParent(i);
i /= 2;
}
node[i].setKey(key);
}
HeapNode MaxHeap::remove()
{
if (isEmpty()) return NULL;
HeapNode item = node[1];
HeapNode last = node[size--];
int parent = 1;
int child = 2;
while (child <= size) {
if (child < size && getLeft(parent).getkey() < getRight(parent).getkey())
child++;
if (last.getkey() >= node[child].getkey()) break; // 마지막 노드가 바로윗줄 코드의 더 큰 자식보다 큰경우
else { // 아니면 한단계 아래로 이동
node[parent] = node[child];
parent = child;
child *= 2;
}
}
node[parent] = last;
return item;
}
void MaxHeap::display()
{
for (int i = 1, level = 1; i <= size; i++) {
if (i == level) {
printf("\n");
level *= 2;
}
node[i].display();
}
printf("\n-------------------------------------------");
}
main.cpp
#include <iostream>
#include "MaxHeap.h"
using namespace std;
int main()
{
MaxHeap heap;
heap.insert(10);
heap.insert(5);
heap.insert(30);
heap.insert(8);
heap.insert(9);
heap.insert(3);
heap.insert(7);
heap.display();
// 삭제
heap.remove();
heap.display();
heap.remove();
heap.display();
cout << endl;
return 0;
}결과는 다음과 같다.
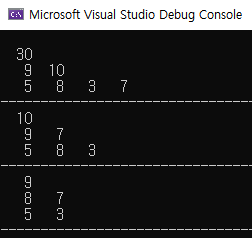
Heap Sort
void heapSort(int a[], int n) {
MaxHeap h;
for (int i = 0; i < n; i++)
h.insert(a[i]);
for (int i = n - 1; i >= 0; i--)
a[i] = h.remove().getkey();
}추가로 허프만 코드에 대하여 배웠다.
나의 현황
◆ 이책은 총 14단원 까지 있다. 하지만 나의 기억상으로 그레프 파트가 어려웠던 기억이 있다. 프로젝트 연습문제 까지 생각하면 약 8일 안에 이책을 끝내도록 노력해봐야 겠다. 이책이 1회독 끝나면 자료구조 복습은 이석호 교수님이 번역해 놓으신 자료구조론 2판을 한 6개월 잡고 틈틈이 복습할 예정이다.
'CS > Data Structure (2021-1)' 카테고리의 다른 글
| [자료구조] C++로 쉽게 풀어쓴 자료구조 : 12장, 가중치 그래프 (0) | 2022.01.15 |
|---|---|
| [자료구조] C++로 쉽게 풀어쓴 자료구조 : 11장, 그래프 (0) | 2022.01.15 |
| [자료구조] C++로 쉽게 풀어쓴 자료구조 프로그래밍 프로젝트 9-1 (0) | 2022.01.15 |
| C++로 쉽게 풀어쓴 자료구조 : 9장, 이진 탐색 트리 (0) | 2022.01.15 |
| C++로 쉽게 풀어쓴 자료구조 프로그래밍 프로젝트 8 (0) | 2022.01.14 |

댓글