직접 풀어보고 올리는 코드입니다. 지적이나 더 좋은 방향에 대한 댓글은 항상 환영합니다.
생각의 흐름
우선 이번문제는 저의 머리로는 생각하지 못한 방식이라 다른 분들의 글들을 확인하면서 해결하였습니다.
정리라도 잘 해놓기 위해 글을 작성해 봅니다.
현재의 피보나치 수와 이전 피보나치 수를 각각 1행, 2행에 배치한 2X1 행렬을 생각해보자.
다음으로 오는 피보나치 수를 구하려면 두 수를 더한 수를 첫 번째 행에, 기존의 첫 번째 행에 있던 피보나치 수는 두 번째 행으로 이동시킨다
이런 동작은 아래와 같은 행렬 곱셉으로 간단하게 수행할 수 있다.

즉, 점화식을 행렬로 만들어 보면 다음과 같아진다.

Fn+2 즉, 다음으로 오는 피보나치 수는 (Fn+1) + Fn 이 됩니다. 현재의 피보나치 수와 직전의 피보나치 수를 더한 것 이죠!
위 행렬식을 다음과 같이 확잘할수가 있습니다.
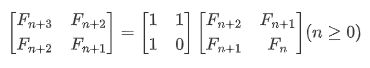
각 행렬을 세로 중심으로 살펴보면 다음과 같을 뿐 입니다.
(n+2 번째 행렬식) (n+1 번째 행렬식) = (연산) (n+1 번째 행렬식) (n 번째 행렬식)
각 행렬을 An으로 치환하면 다음과 같이 나타낼수 있습니다.

A0 가 {1,1,1,0}이므로 An은 {1,1,1,0}의 n 거듭제곱 꼴로 나타낼수 있겠죠?

다시 An을 치환하면 다음과 같아집니다.

이렇게 구한 점화식으로 분할정복을 해 나가면 됩니다!
우선 행렬의 곱셈을 위해서 연산자 오버로딩을 진행해 주어야 합니다. 곱셈에 대한 오버로딩이 필요합니다!
typedef vector<vector<long long> > matrix;
matrix operator*(matrix &a, matrix &b) {
matrix temp(2, vector<long long>(2)); // long long 2개로 초기화 된 vector를 2개 갖는 temp matrix vector
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
for (int k = 0; k < 2; k++) {
temp[i][j] += a[i][k] * b[k][j];
}
temp[i][j] %= MOD;
}
}
return temp;
}
이제 분할 정복을 어떻게 해결할지 설명해 보겠습니다.
예를 들어 n=1024로 주어진다고 생각해보죠!
Loop 1)
a = [[1,1],[1,0]]^2 이고 n = 512
Loop 2)
a = [[1,1],[1,0]]^4 이고 n = 256
Loop 3)
a = [[1,1],[1,0]]^8 이고 n = 128
Loop 4)
a = [[1,1],[1,0]]^16 이고 n = 64
Loop 5)
a = [[1,1],[1,0]]^32 이고 n = 32
Loop 6)
a = [[1,1],[1,0]]^64 이고 n = 16
Loop 7)
a = [[1,1],[1,0]]^128 이고 n = 8
Loop 8)
a = [[1,1],[1,0]]^256 이고 n = 4
Loop 9)
a = [[1,1],[1,0]]^512 이고 n = 2
Loop 10)
a = [[1,1],[1,0]]^1024 이고 n = 1 이 되니, 나머지 연산을 진행하여 n%2 로 결과값이 1이 되니 정답을 저장하면 됩니다.
matrix ans = {{1, 0},
{0, 1}};
matrix a = {{1, 1},
{1, 0}};
while (n > 0) {
if (n % 2 == 1) {
ans = ans * a;
}
a = a * a;
n /= 2;
}
나의 코드
#include <bits/stdc++.h>
using namespace std;
#define MAX 100001
#define MOD 1000000007
long long n;
typedef vector<vector<long long> > matrix;
matrix operator*(matrix &a, matrix &b) {
matrix temp(2, vector<long long>(2)); // long long 2개로 초기화 된 vector를 2개 갖는 temp matrix vector
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
for (int k = 0; k < 2; k++) {
temp[i][j] += a[i][k] * b[k][j];
}
temp[i][j] %= MOD;
}
}
return temp;
}
int main() {
ios_base::sync_with_stdio(0);
cin.tie(0);
cin >> n;
matrix ans = {{1, 0},
{0, 1}};
matrix a = {{1, 1},
{1, 0}};
while (n > 0) {
if (n % 2 == 1) {
ans = ans * a;
}
a = a * a;
n /= 2;
}
cout << ans[0][1] << '\n';
return 0;
}'Algorithm > 백준' 카테고리의 다른 글
| [백준][C++] 5693번: 이진 검색 트리 <197> (0) | 2022.03.08 |
|---|---|
| [백준][C++] 1865번: 웜홀 <196> (0) | 2022.03.06 |
| [백준][C++] 2749번: 피보나치 수 3 <194> (0) | 2022.03.02 |
| [백준][C++] 9471번: 피사노 주기 <193> (0) | 2022.03.01 |
| [백준][C++] 10826번: 피보나치 수 4 <192> (0) | 2022.03.01 |

댓글