해당 본문은 학교수업시간에 배운 강의내용을 기반으로 정리하는 요약글 입니다. 정확하지 않은 점이 있으면 지적해주시면 감사하겠습니다.
원래 Merget Sort를 증명하려면 Merge의 정확성 부터 증명한 후, 다시 Merge sort를 증명해야하는데, 수업시간에는 Merge의 정확성은 타당하다는 가정 하에 증명해 주셨다. Merge의 정확성 까지 보일필요는 없을거라 하셨다.
Recursive Merge Sort 의 증명
int MergeSort(int a[], int n) {
int h;
int b[n];
h = n / 2;
// copy a[] to b[]
MergeSort(b, h); // b의 왼쪽 절반 정렬
MergeSort(b+h, n-h); // b의 오른쪽 절반 정렬
// Merge two halves in b to a
return 0;
}전체 코드를 보일까 하다가 구현이 목적인 글은 아니고 또 어짜피 구글 찾아보면 널린게 코드이니 이는 패스 하겠다.
우선 그림을 통해 전체적인 느낌을 먼저 느껴보자.
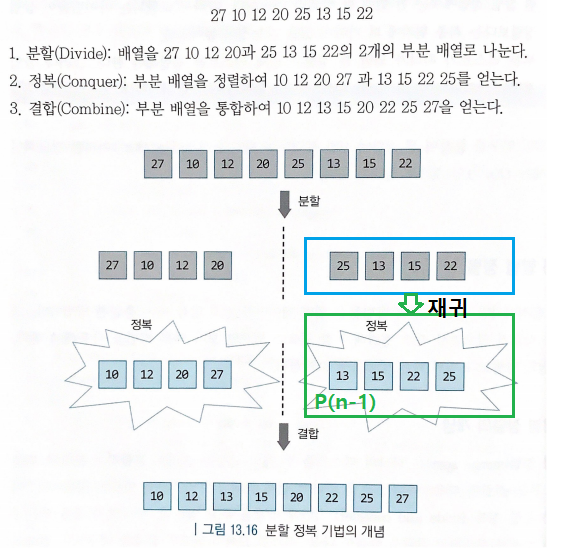
위의 사진에서 하늘색 박스에서 초록색 박스로 바뀌는 지점이 재귀가 작동하는 부분이다.
그냥 재귀에 의해서 파란박스가 정렬된 초록박스처럼 바뀐다고 믿으면 된다. 이는 귀납법에 의해 타당하다.
재귀의 문제이니 이를 귀납법으로 간단하게 증명할 수 있다.
우선 집합 조건을 깰 수 있는 코드는 없다. (sorting의 증명은 집합조건도 확인해 주자!)
(1) Base: P(1)이 참임을 보여야한다.
P(1)은 당연하게 참이다. n=1이라는 말은 원소가 1개라는 말인데, 원소가 1개이면 항상 정렬되어있다.
(2) Step: P(n-1) -> p(n) 이 참이라면
P(n-1)이 참이라 믿으면, 즉 n/2의 범위에서 MergeSort() 를 호출한후 sorting이 성공한다고 믿으면 (이는 위의 사진의 파란박스가 초록박스로 바뀌는 논리와 동일하다)
=> 재귀 호출이 끝난후 (1) a[0] < a[1] < ... < a[n/2 - 1] and (2) a[n/2] < a[n/2 + 1] < ... < a[n-1] 이 성립한다고 믿으면
P(n)일때 즉, n일때 MergeSort()가 성공한다.
=> 재귀 호출이 끝난후(3) a[0] < a[1] < ... < a[n - 1] 성립
이때 (1) 과 (2) 를 통해 (3) 을 도출할수 있는 근거는 Merge의 정확성 으로부터 나온다.
(3) Result: P(n)은 모든 자연수 n에 대해서 참이다.
Complexity
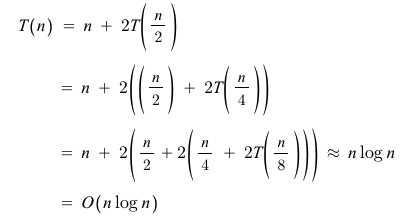
'CS > Data Structure (2021-1)' 카테고리의 다른 글
| [자료구조] String Matching (0) | 2022.01.24 |
|---|---|
| [자료구조] 배열의 성능 분석 (0) | 2022.01.24 |
| [자료구조] Selection Sort 증명 (0) | 2022.01.22 |
| [자료구조] Binary Search 증명 (5) | 2022.01.22 |
| [자료구조] 수학적 귀납법 증명 (2) | 2022.01.22 |

댓글