직접 풀어보고 올리는 코드입니다. 지적이나 더 좋은 방향에 대한 댓글은 항상 환영합니다.
14852번: 타일 채우기 3
첫째 줄에 경우의 수를 1,000,000,007로 나눈 나머지를 출력한다.
www.acmicpc.net
생각의 흐름
맨 처음 생각했던 방식은 DP[N]을 만들기 위해 끝부분에 2*1 채우는 방식과, 2*2
즉, 다음 그림과 같은 방식이 끝이라고 생각했다.
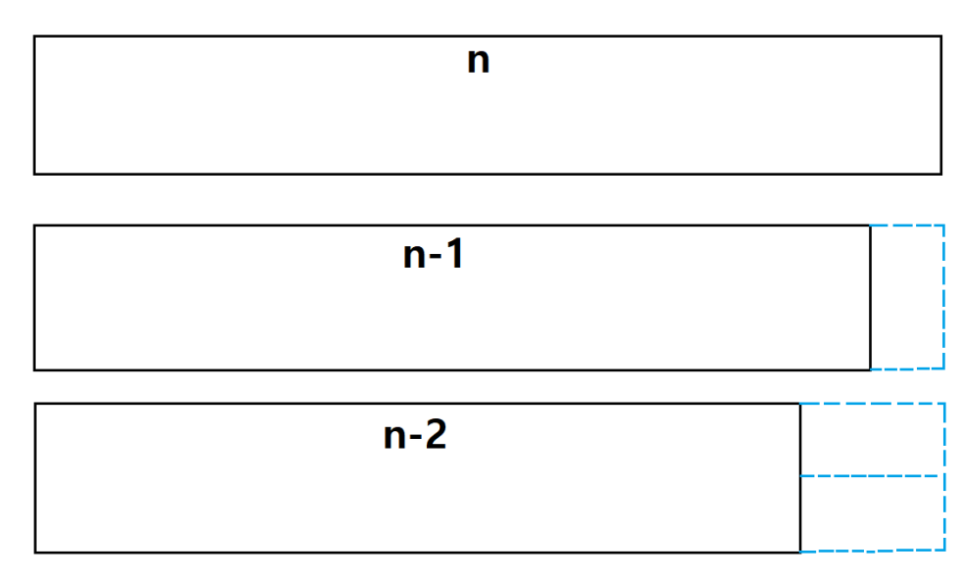
따라서 점화식이 DP[N] = DP[N-1]*2 + DP[N-2]*3 이라 생각했다.
하지만 예외가 있었다. 길이가 3, 4, 5 ... 등 다음과 같은 추가적인 case가 존재했다.

각각 길이가 3, 4인 case 이다.
즉 DP[N] = DP[N-1]*2 + DP[N-2]*3 + DP[N-3]*2 + DP[N-4]*2 + ... + DP[1] * 2 까지 가능한것 이다.
따라서 DP[N-3]*2 + DP[N-4]*2 + ... + DP[1] * 2 의 합을 DP[N][1]로 표현하기로 하자.
DP[n][0]은 딱 DP의 해당 값을 의미하고,
DP[n][1]은 DP[n-3]부터 DP[1] 까지의 총 합을 의미한다.
=> DP[N][0] = DP[N-1][0]*2 + DP[N-2][0]*3 + DP[N][1] * 2
그럼 DP[N][1]은 어떻게 구할까?
DP[N-3]*2 + DP[N-4]*2 + ... + DP[1] * 2 을 분리하면 (DP[N-3]*2) + (DP[N-4]*2 + ... + DP[1] * 2) 으로 생각할수가 있다.
즉 DP[N][1] = DP[N-3][0] + DP[N-1][1]이 되게 돤다.
나의 코드
#include <bits/stdc++.h>
using namespace std;
#define MAX 1000001
#define MOD 1000000007
int N;
int arr[MAX];
long long DP[MAX][2];
int main(){
ios_base::sync_with_stdio(0);
cin.tie(0);
cin >> N;
DP[1][0] = 2;
DP[2][0] = 7;
DP[2][1] = 1;
for(int i = 3; i <= N; i++){
DP[i][1] = (DP[i-3][0] + DP[i-1][1]) % MOD;
DP[i][0] = (DP[i-1][0]*2 + DP[i-2][0]*3 + DP[i][1]*2) % MOD;
}
cout << DP[N][0] % MOD;
return 0;
}'Algorithm > 백준' 카테고리의 다른 글
| [백준][C++] 3980번: 선발 명단 <181> (0) | 2022.02.03 |
|---|---|
| [백준][C++] 12919번: A와 B 2 <180> (0) | 2022.01.31 |
| [백준][C++] 2573번: 빙산 <179> (0) | 2022.01.26 |
| [백준][C++] 13397번: 구간 나누기 2 <178> (0) | 2022.01.25 |
| [백준][C++] 17135번: 캐슬 디펜스 <176> (0) | 2022.01.19 |

댓글